(a) For angle AFB
$\tan \angle AFB = \dfrac{AB}{BF}$
$\tan \angle AFB = \dfrac{10}{15}$
$\angle AFB = 33^\circ 41'$ answer
For angle BFO
$BD = \sqrt{AB^2 + AD^2}$
$BD = \sqrt{20^2 + 10^2}$
$BD = 10\sqrt{5} \, \text{ in}$
$OB = \frac{1}{2}BD$
$OB = \frac{1}{2}(10\sqrt{5})$
$OB = 5\sqrt{5} \, \text{ in}$
$\tan \angle BFO = \dfrac{OB}{BF}$
$\tan \angle BFO = \dfrac{5\sqrt{5}}{15}$
$\angle BFO = 36^\circ 42'$ answer
For angle AFO
$OA = OB$
$OA = 5\sqrt{5} \, \text{ in}$
$OA^2 = 125$
$AF^2 = AB^2 + BF^2$
$AF^2 = 10^2 + 15^2$
$AF^2 = 325$
$AF = 5\sqrt{13} \, \text{ in}$
$OF^2 = OB^2 + BF^2$
$OF^2 = (5\sqrt{5})^2 + 15^2$
$OF^2 = 350$
$OF = 5\sqrt{14} \, \text{ in}$
Apply cosine law to triangle AFO
$OA^2 = AF^2 + OF^2 - 2(AF)(OF)\cos \angle AFO$
$125 = 325 + 350 - 2(5\sqrt{13})(5\sqrt{14})\cos \angle AFO$
$\cos \angle AFO = \dfrac{325 + 350 - 125}{2(5\sqrt{13})(5\sqrt{14})}$
$\angle AFO = 35^\circ 23'$ answer
For angle BOF
$\tan \angle BOF = \dfrac{BF}{OB}$
$\tan \angle BOF = \dfrac{15}{5\sqrt{5}}$
$\angle BOF = 53^\circ 18'$ answer
Another solution
$\angle BOF = 90^\circ - \angle BFO$
$\angle BOF = 90^\circ - 36^\circ 42'$
$\angle BOF = 53^\circ 18'$ okay
For angle AOF
Cosine law for triangle AOF
$AF^2 = OA^2 + OF^2 - 2(OA)(OF)\cos \angle AOF$
$325 = 125 + 350 - 2(5\sqrt{5})(5\sqrt{14})\cos \angle AOF$
$\cos \angle AOF = \dfrac{125 + 350 - 325}{2(5\sqrt{5})(5\sqrt{14})}$
$\angle AOF = 68^\circ 59'$ answer
For angle OFC
$CF^2 = BC^2 + BF^2$
$CF^2 = 20^2 + 15^2$
$CF^2 = 625$
$CF = 25 \, \text{ in}$
$OC = OA$
$OC = 5\sqrt{5} \, \text{ in}$
$OC^2 = 125$
Cosine law for triangle OFC
$OC^2 = OF^2 + CF^2 - 2(OF)(CF)\cos \angle OFC$
$125 = 350 + 625 - 2(5\sqrt{14})(25)\cos \angle OFC$
$\cos \angle OFC = \dfrac{350 + 625 - 125}{2(5\sqrt{14})(25)}$
$\angle OFC = 24^\circ 40'$ answer
(b) For triangle ABO
$A_{ABO} = \frac{1}{2}(10)(10)$
$A_{ABO} = 50 \, \text{ in}^2$ answer
For triangle BOF
$A_{BOF} = \frac{1}{2}(OB)(BF)$
$A_{BOF} = \frac{1}{2}(5\sqrt{5})(15)$
$ABOF = 83.85 \, \text{ in}^2$ answer
For triangle AOF
$A_{AOF} = \frac{1}{2}(OA)(OF)\sin \angle AOF$
$A_{AOF} = \frac{1}{2}(5\sqrt{5})(5\sqrt{14})\sin 68^\circ 59'$
$A_{AOF} = 97.62 \, \text{ in}^2$
(c) Distance from B to the plane AOF.
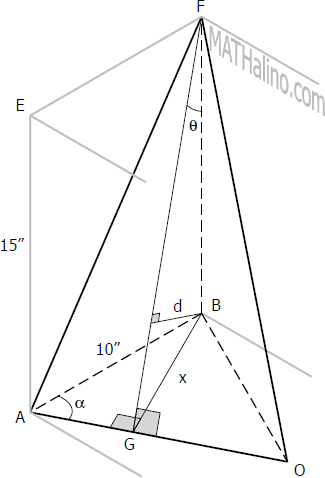Triangles ABC and AGB are similar
$sin \alpha = \dfrac{BC}{AC} = \dfrac{BG}{AB}$
$\dfrac{20}{\sqrt{10^2 + 20^2}} = \dfrac{x}{10}$
$x = 4\sqrt{5}$
$\tan \theta = \dfrac{x}{BF}$
$\tan \theta = \dfrac{4\sqrt{5}}{15}$
$\theta = 30.81^\circ$
$\sin \theta = \dfrac{d}{BF}$
$d = BF \sin \theta$
$d = 15 \sin 30.81^\circ$
$d = 7.682 \, \text{ in}$ answer
