The Sphere

Sphere is a solid bounded by closed surface every point of which is equidistant from a fixed point called the center.
 

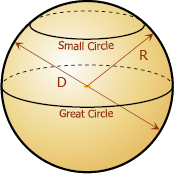
Sphere with small and great circles shown

 

Properties of a Sphere

  • Every section in the sphere made by a cutting plane is a circle. If the cutting plane passes through the center of the sphere, the section made is a great circle; otherwise the section is a small circle.
  • For a particular circle of a sphere, the axis is the diameter of the sphere perpendicular to the plane of the circle.
  • The ends of the axis of the circle of a sphere are called poles.
  • The nearer the circle to the center of the sphere, the greater is its area.
  • The largest circle in the sphere is the great circle.
  • The radius (diameter) of the great circle is the radius (diameter) of the sphere.
  • All great circles of a sphere are equal.
  • Every great circle divides the sphere into two equal parts called hemispheres.
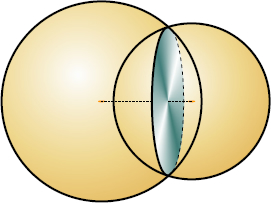  • Two intersecting spheres form a circular sectionThe intersection of two spherical surfaces is a circle whose plane is perpendicular to the line joining the centers of the spheres and whose center is on that line. (See figure to the right.)
  • A plane perpendicular to a radius at its extremity is tangent to the sphere.

 

Formulas for a Sphere

Surface Area, A
The surface area of a sphere is equal to the area of four great circles.
$A = 4\pi R^2$

$A = \pi D^2$

 

Volume, V

$V = \frac{4}{3}\pi R^3$

$V = \frac{1}{6}\pi D^3$