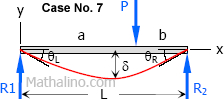
From
Case No. 7 of
Summary of Beam Loadings, the deflection equations are
$EI \, y = \dfrac{Pbx}{6L}(L^2 - x^2 - b^2) \text{ for } 0 \lt x \lt a$
$EI \, y = \dfrac{Pb}{6L} \left[ \dfrac{L}{b}(x - a)^3 + (L^2 - b^2)x - x^3 \right] \text{ for } a \lt x \lt L$
The point under the load $P$ is generally located at $x = a$ and at this point, both equations above will become
$EI \, y = \dfrac{Pab}{6L}(L^2 - a^2 - b^2)$
Deflection under the 500 N load
EIδ = EIδ due to 500 N load + EIδ due to 800 N load
$EI \, \delta = \dfrac{500(2)(3)}{6(5)}(5^2 - 2^2 - 3^2) + \dfrac{800(1)(2)}{6(5)}(5^2 - 2^2 - 1^2)$
$EI \, \delta = 1200 + 1066.67$
$EI \, \delta = 2266.67 \, \text{ N}\cdot\text{m}^3$ answer
Deflection under the 800 N load
EIδ = EIδ due to 500 N load + EIδ due to 800 N load
$EI \, \delta = \dfrac{500(3)}{6(5)} \left[ \dfrac{5}{3}(4 - 2)^3 + (5^2 - 3^2)(4) - 4^3 \right] + \dfrac{800(1)(4)}{6(5)}(5^2 - 4^2 - 1^2)$
$EI \, \delta = 666.67 + 853.33$
$EI \, \delta = 1520 \, \text{ N}\cdot\text{m}^3$ answer
