College Algebra

Real Numbers, $\mathbb{R}$
Complex numbers, $\mathbb{C}$
1. Imaginary Numbers
Laws of Indices
Properties of Radicals
Properties of Logarithm
Special Products and Factoring
The Quadratic Equation
1. The Quadratic Formula
  1. Discriminant
  2. Sum and Product of Roots
Sequences and Series

Real Numbers, $\mathbb{R}$

Real numbers includes all the numbers in the number line. It is denoted by $\mathbb{R}$.

Integers, $\mathbb{Z}$
Includes all positive and negative whole numbers. $\mathbb{Z} = \left\{ \ldots, -3, -2, -1, 0, 1, 2, 3, \ldots \right\}$
Natural numbers, $\mathbb{N}$
All of positive integers including zero. Also called counting numbers. $\mathbb{N} = \left\{ 0, 1, 2, 3, \ldots \right\}$
Rational numbers, $\mathbb{Q}$
If $a$ and $b$ are integers and $b \ne 0$, then $\dfrac{a}{b}$ is a rational number. As $b$ can take the value of $1$, all integers are rational numbers.
Irrational numbers, $\mathbb{I}$
Real numbers that cannot be expressed as a fraction of integers are irrational numbers. Example, $\mathbb{I} = { \pi, e, \sqrt{7}, \dots }$

Properties of Real Numbers

Let $a$, $b$, and $c$ be any real number.

Closure Property of Addition
$a + b$ is equal to another real number unique from $a$ and $b$.
Closure Property of Multiplication
$a \times b$ is equal to another real number unique from $a$ and $b$.
Commutative Property of Addition
$a + b = b + a$
Commutative Property of Multiplication
$a \times b = b \times a$
Associative Property of Addition
$a + b + c = (a + b) + c = a + (b + c) = (a + c) + b$
Associative Property of Multiplication
$a \times b \times c = (ab)c = a(bc) = c(ab)$
Distributive Property
$a(b + c) = ab + ac$

Absolute Value of Real Numbers

In the number line, the absolute value of any number is the distance between $0$ and the number.

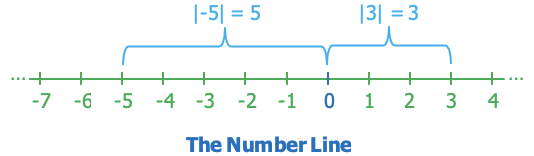
The absolute value of $a$ is denoted by $\lvert a \rvert$.

Properties of Absolute Value

$\lvert \pm a \rvert = a$
$\lvert 0 \rvert = 0$
$\lvert a \rvert = \lvert -a \rvert$
$\lvert a - b \rvert = \lvert b - a \rvert$
If $\lvert x \rvert = a$ then $x = -a$ or $x = a$, where $a$ is a positive number.

Operation of Real Numbers

If $a$ and $b$ are positive and $a \gt b$, then ...

Addition
1. $a + b = \lvert a + b \rvert$
2. $(-a) + (-b) = - \lvert a + b \rvert$
Subtraction
1. $a - b = a + (-b)$
2. $a - b = \lvert a - b \rvert$
3. $b - a = - \lvert a - b \rvert$
4. $(-a) - (-b) = - \lvert a - b \rvert$
5. $(-b) - (-a) = \lvert a - b \rvert$
Multiplication
1. $ab = (-a)(-b) = \lvert ab \rvert$
2. $a(-b) = (-a)b = - \lvert ab \rvert$
3. $ab = 0$ if $a = 0$ or $b = 0$ or both $a$ and $b$ are zero.
Division
1. $\dfrac{a}{b} = \dfrac{-a}{-b} = \left| \dfrac{a}{b} \right|$
2. $\dfrac{-a}{b} = \dfrac{a}{-b} = - \left| \dfrac{a}{b} \right|$
3. $\dfrac{0}{\pm a} = 0$
4. $\dfrac{\pm a}{0} = \infty$

Equality of Real Numbers

For all real numbers $a$, $b$, and $c$ ...

Symmetric Property
$a = b$ then $b = a$
Transitive Property
If $a = b$ and $b = c$ then $a = c$
Addition Property of Equality
$a = b$ iff $a + c = b + c$
Multiplication Property of Equality
$a = b$ iff $ac = bc$, given that $c \ne 0$.

Note: iff means "if and only if".

Inequality of Real Numbers

Symbol	Statement
$a \gt b$	$a$ is greater than $b$
$a \lt b$	$a$ is less than $b$
$a \ge b$	• $a$ is greater than or equal to $b$ • $a$ is at least $b$
$a \le b$	• $a$ is less than or equal to $b$ • $a$ is at most $b$

Properties of Inequality

For all real numbers $a$, $b$, and $c$ ...

If $a \gt b$ then $b \lt a$ and $-a \lt -b$
If $a \gt 0$ then $-a \lt 0$ and if $a \lt 0$ then $-a \gt 0$
Addition Property of Inequality
$a \gt b$ iff $a + c \gt b + c$
Multiplication Property of Inequality
1. $a \gt b$ iff $ac \gt bc$ when $c \gt 0$
2. $a \gt b$ iff $ac \lt bc$ when $c \lt 0$
If $\lvert x \rvert \lt a$ then $x \gt -a$ and $x \lt a$, where $a$ is a positive number.
If $\lvert x \rvert \gt a$ then $x \lt -a$ or $x \gt a$, where $a$ is a positive number.

Complex numbers, $\mathbb{C}$

Complex numbers are in the form $a + bi$, where $a$ is the real part and $bi$ is the imaginary part. Note that $a$ and $b$ are real numbers.

Imaginary Numbers

The $\sqrt{-1}$ is called the imaginary unit and is denoted by $i$. Imaginary number is a product of a real number and $i$. Example: $5i$, $\sqrt{2} i$, $\pi i$.

$i = \sqrt{-1}$ or $i^2 = -1$

Laws of Indices

$b^n = \underbrace{b \cdot b \cdot b \cdot \ldots}_{n \text{ factors of } b}$
$a^m \cdot a^n = a^{m + n}$
$(a^m)^n = a^{mn}$
$\dfrac{a^m}{a^n} = a^{m - n}$
$(abc)^n = a^n \cdot b^n \cdot c^n$
$\left( \dfrac{a}{b} \right)^n = \dfrac{a^n}{b^n}$
$a^{-n} = \dfrac{1}{a^n}$ and $\dfrac{1}{a^{-n}} = a^n$
$a^0 = 1$
If $a^m = a^n$ then $m = n$ provided $a \ne \left\{ 0, 1, -1 \right\}$

Properties of Radicals

$a^{1/n} = \sqrt[n]{a}$
$a^{m/n} = \sqrt[n]{a^m} = \left( \sqrt[n]{a} \right)^m$
$\sqrt[m]{a} \cdot \sqrt[n]{a} = \sqrt[mn]{a^{m + n}}$
$\sqrt[n]{a} \cdot \sqrt[n]{b} = \sqrt[n]{ab}$
$\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\dfrac{a}{b}}$ provided $b \ne 0$
$\left( \sqrt[n]{a} \right)^n = a$

Properties of Logarithm

If $y = b^x$, then $x = \log_b y$
$\log_b (xyz) = \log_b x + \log_b y + \log_b z$
$\log_b \left( \dfrac{x}{y} \right) = \log_b x - \log_b y$
$\log_b x^n = n \log_b x$
$b^{\log_b x} = x$
$\log_b 1 = 0$
$\log_b b = 1$
Common Logarithm
$\log_{10} x = \log x$
Natural Logarithm
$\log_e x = \ln x$

The Euler's number $e$ is approximately 2.71828, an irrational number. The exact value of $e$ in infinite series is $\displaystyle e = \sum_{n = 0}^\infty \dfrac{1}{x!}$. In Calculus, the number $\displaystyle e = \lim_{n \to \infty} \left( 1 + \dfrac{1}{n} \right)^n$.
Change-base Rule
$\log_y x = \dfrac{\log x}{\log y} = \dfrac{\ln x}{\ln y}$
If $\log_b x = \log_b y$ then $x = y$

Special Products and Factoring

Special Products

$(x + y)(x - y) = x^2 - y^2$
$(x + y)^2 = x^2 + 2xy + y^2$
$(x - y)^2 = x^2 - 2xy + y^2$
$(x + y)^3 = x^3 + 3x^2y + 3xy^2 + y^3$
$(x - y)^3 = x^3 - 3x^2y + 3xy^2 - y^3$
$(x + a)(x + b) = x^2 + (a + b)x + ab$
$(ax + by)(cx + dy) = acx^2 + (ad + bc)xy + bdy^2$

Factoring Polynomials

$ax + ay + az = a(x + y + z)$
$x^2 - y^2 = (x + y)(x - y)$
$x^3 + y^3 = (x + y)(x^2 - xy + y^2)$
$x^3 - y^3 = (x - y)(x^2 + xy + y^2)$
$x^2 + 2xy + y^2 = (x + y)^2$
$x^2 - 2xy + y^2 = (x - y)^2$
$x^2 + (a + b)x + ab = (x + a)(x + b)$
$acx^2 + (ad + bc)xy + bdy^2 = (ax + by)(cx + dy)$

Expansion of $(a + b)^n$

This is called the Binomial Theorem. The r^th term in the expansion of (a + b)ⁿ is given by the formula:

$r^{th} \, \text{term} = {_nC_m} \, a^{n - m} b^m$

where m = r - 1

The Quadratic Equation

The quadratic equation is inthe form $Ax^2 + Bx + C = 0$ and can be written in a factored form $(x - x_1)(x - x_2) = 0$, where $x_1$ and $x_2$ are the roots of the quadratic equation.

The Quadratic Formula

$x = \dfrac{-B \pm \sqrt{B^2 - 4AC}}{2A}$

Discriminant

The quantity $B^2 - 4AC$ inside the $\sqrt{~}$ of the quadratic formula is called the discriminant. The nature of roots of the quadratic equation according the value of discriminant are as follows:

There is only 1 root if $B^2 - 4AC = 0$.
The roots are two unequal numbers if $B^2 - 4AC \gt 0$.
The roots are imaginary if $B^2 - 4AC \lt 0$.

Sum and Product of Roots

Sum of roots
$x_1 + x_2 = -\dfrac{B}{A}$
Product of roots
$x_1 \cdot x_2 = \dfrac{C}{A}$

Sequences and Series

Sequence is a succession of numbers formed according to some fixed rule.
$$1, 4, 9, 16, 25, \ldots$$

is a sequence whose $n^\text{th}$ term is equal to $n^2$
Series is the indicated sum of a sequence of numbers.
$$1 + 4 + 9 + 16 + 25 + \ldots = \sum_{n = 1}^\infty n^2$$

is an example of a series.

Arithmetic Progression, AP

A sequence of numbers is in AP if any number after the first is obtained by adding a fixed number to the one immediately preceding it. The fixed number that is added is called the common difference, $d$.

Common difference
$d = a_2 - a_1 = a_3 - a_2 = a_4 - a_3 = \ldots$
$n^\text{th}$ term
$a_n = a_1 + (n - 1)d$
Sum of first $n$ terms
$S = \frac{1}{2}n(a_1 + a_n)$

$S = \frac{1}{2}n \left[ 2a_1 + (n - 1)d \right]$

Geometric Progression, GP

A sequence of numbers is in GP if any number after the first is obtained by multiplying a fixed number to the one immediately preceding it. The fixed number that is multiplied is called the common ratio, $r$.

Common ratio
$r = \dfrac{a_2}{a_1} = \dfrac{a_3}{a_2} = \dfrac{a_4}{a_3} = \ldots$
$n^\text{th}$ term
$a_n = a_1 r^{n - 1}$
Sum of first $n$ terms
$S = \dfrac{a_1(1 - r^n)}{1 - r}$ ← for $r \lt 1$

$S = \dfrac{a_1(r^n - 1)}{r - 1}$ ← for $r \gt 1$

Infinite Geometric Progression, IGP

Infinite Geometric Progression is a GP in which $-1 \lt r \lt 1$, $r \ne 0$ and $n \to \infty$. The sum of IGP is given by the formula

$$S = \dfrac{a_1}{1 - r}$$

Harmonic Progression, HP

A sequence of numbers are in HP if their reciprocals form an AP.

Common difference of reciprocals
$\dfrac{1}{a_2} - \dfrac{1}{a_1} = \dfrac{1}{a_3} - \dfrac{1}{a_2} = \dfrac{1}{a_4} - \dfrac{1}{a_3} = \ldots$
$n^\text{th}$ term
$a_n = \dfrac{1}{a_1 + (n - 1)d}$
Sum of first $n$ terms
$S = \dfrac{1}{d} ~ \ln \left[ \dfrac{2a_1 + (2n - 1)d}{2a_1 - d} \right]$

Contents