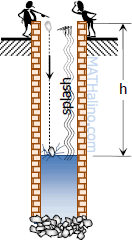
$t_{stone} + t_{sound} = 5$
For tstone (free-falling body):
$h = \frac{1}{2}gt^2$
$t = \sqrt{\dfrac{2h}{g}}$
For tsound (uniform motion):
$h = vt$
$t = \dfrac{h}{v}$
Thus,
$\sqrt{\dfrac{2h}{g}} + \dfrac{h}{v} = 5$
English System
$\sqrt{\dfrac{2h}{32.2}} + \dfrac{h}{1120} = 5$
$\sqrt{\dfrac{2h}{32.2}} = 5 - \dfrac{h}{1120}$
$\dfrac{2h}{32.2} = \left( 5 - \dfrac{h}{1120} \right)^2$
$\dfrac{10h}{161} = 25 - \dfrac{h}{112} + \dfrac{h^2}{1\,254\,400}$
$\dfrac{1}{1\,254\,400}h^2 - \dfrac{183}{2576}h + 25 = 0$
$h = 88\,759.73 \, \text{ and } \, 353.31$
For h = 88 759.73 ft
$t = \sqrt{\dfrac{2(88\,759.73)}{32.2}}$
$t = 74.2 ~ \text{sec} ~ \gt 5 ~ \text{sec}$ (not okay!)
For h = 353.31 ft
$t = \sqrt{\dfrac{2(353.31)}{32.2}}$
$t = 4.68 ~ \text{sec} ~ \lt 5 ~ \text{sec}$ (okay!)
Thus, h = 353.31 ft → answer
SI Units
$\sqrt{\dfrac{2h}{9.81}} + \dfrac{h}{341.376} = 5$
$\sqrt{\dfrac{2h}{9.81}} = 5 - \dfrac{h}{341.376}$
$\sqrt{\dfrac{200h}{981}} = 5 - \dfrac{125h}{42\,672}$
$\dfrac{200h}{981} = \left( 5 - \dfrac{125h}{42\,672} \right)^2$
$\dfrac{200h}{981} = 25 - \dfrac{625h}{21\,336} + \dfrac{15\,625h^2}{1\,820\,899\,584}$
$\dfrac{15\,625}{1\,820\,899\,584}h^2 - \dfrac{1\,626\,775}{6\,976\,872}h + 25 = 0$
$h = 27\,065.05 \, \text{ and } \, 107.64$
For h = 27 065.05 m
$t = \sqrt{\dfrac{2(27\,065.05)}{9.81}}$
$t = 74.2 ~ \text{sec} ~ \gt 5 ~ \text{sec}$ (not okay!)
For h = 107.64 m
$t = \sqrt{\dfrac{2(107.64)}{9.81}}$
$t = 4.68 ~ \text{sec} \lt 5 ~ \text{sec}$ (okay!)
Thus, h = 107.64 m → answer
