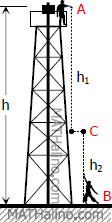
h = 24.38 m
v
A = 0
v
B = 12.19 m/s
g = 9.81 m/s
2
From A to C (free-fall)
$h_1 = \frac{1}{2}gt^2$
$h_1 = \frac{1}{2}(9.81)t^2$
$h_1 = 4.905t^2$
From B to C (upward motion)
From the formula s = vit + ½ at2
$h_2 = v_Bt - \frac{1}{2}gt^2$
$h_2 = 12.19t - \frac{1}{2}(9.81)t^2$
$h_2 = 12.19t - 4.905t^2$
A to C plus B to C is equal to height of the tower
$h_1 + h_2 = h$
$4.905t^2 + (12.19t - 4.905t^2) = 24.38$
$12.19t = 24.38$
$t = 2 \, \text{ sec}$
$h_1 = 4.905(2^2)$
$h_1 = 19.62 \, \text{ m}$
They pass each other after 2 seconds at 19.62 m from the top of the tower. answer
Velocity at C of stone from A (after 2 seconds)
$v_{C1} = gt = 9.81(2)$
$v_{C1} = 19.62 \, \text{ m/s}$
Velocity at C of stone from B (after 2 seconds)
$v_{C2} = v_B - gt = = 12.19 - 9.81(2)$
$v_{C2} = -7.43 \, \text{ m/s}$ → the negative sign indicates that the stone is now moving downward
Relative velocity:
$v_r = v_{C1} + v_{C2} = 19.62 - 7.43$
$v_r = 12.19 \, \text{ m/sec}$ answer
