Curvilinear Translation (Projectile Motion)

Projectile motion follows a parabolic trajectory. The vertical component of projectile is under constant gravitational acceleration and the horizontal component is at constant velocity. For easy handling, resolve the motion into x and y components and use the formulas in rectilinear translation.
 

Form the figure below:

$v_{ox} = v_o \, \cos \theta$

$v_{oy} = v_o \, \sin \theta$

 

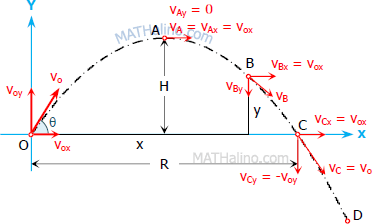
000-projectile-general.gif

 

At any point B

For the x-component of motion, acceleration is zero (constant velocity), thus ax = 0.
$v_{Bx} = v_{ox}$

$x = v_{ox}t$

 

For the y-component of motion, ay = -g. Notice that the first three formulas that follow are taken from motion with constant acceleration.

$v_{By} = v_{oy} - gt$

$y = v_{oy}t - \frac{1}{2}gt^2$

${v_{By}}^2 = {v_{oy}}^2 - 2gy$

 

From x = voxt, t = x/vox. Substitute t = x/vox to y = voyt - ½ gt2.
$y = v_{oy}\left( \dfrac{x}{v_{ox}} \right) - \frac{1}{2}g\left( \dfrac{x}{v_{ox}} \right)^2$

$y = v_{oy}\left( \dfrac{x}{v_{ox}} \right) - \frac{1}{2}g\left( \dfrac{x^2}{{v_{ox}}^2} \right)$

$y = v_o \, \sin \theta \left( \dfrac{x}{v_o \, \cos \theta} \right) - \frac{1}{2}g\left[ \dfrac{x^2}{(v_o \, \cos \theta)^2} \right]$

$y = \dfrac{x \, \sin \theta}{\cos \theta} - \dfrac{gx^2}{2{v_o}^2 \, \cos^2 \theta}$

$y = x \, \tan \theta - \dfrac{gx^2}{2{v_o}^2 \, \cos^2 \theta}$

 

At point A

At the highest point or summit, vAy = 0.
$H = \dfrac{{v_{oy}}^2}{2g}$

$t = \dfrac{v_{oy}}{g}$

 

At point C

x = R, y = 0, vC = vo, and vy = -voy
$R = \dfrac{{v_o}^2 \, \sin \, 2\theta}{g}$

$t = \dfrac{2v_{oy}}{g} = \dfrac{2v_o \, \sin \theta}{g}$

 

Note:

  • vy is positive if directed upward and negative if directed downward
  • At any point D below the origin O, the sign of y is negative.

 

Tags
projectile
curvilinear motion
formulas for projectile