Burning Bale from Catapult to Travel 150 ft and Clear Over 35 ft Castle Wall

Problem
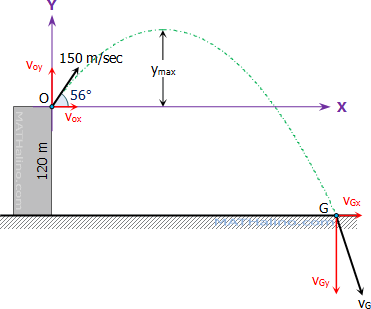
A catapult is placed 100 ft from the castle wall, which is 35 feet high. The soldier wants the burning bale of hay to clear the top of the wall and land 50 feet inside the castle wall. If the initial velocity of the bale is 70 feet per second, then at what angle should the bale of hay be launched so that it travel 150 feet and pass over the castle wall. Use g = 32 ft/sec2.
 

2016-may-math-catapult.jpg

 

A.   49.8° C.   39.2°
B.   50.8° D.   40.2°

 

01 - Highest point of projectile as measured from inclined plane

Problem 01
A projectile is fired up the inclined plane at an initial velocity of 15 m/s. The plane is making an angle of 30° from the horizontal. If the projectile was fired at 30° from the incline, compute the maximum height z measured perpendicular to the incline that is reached by the projectile. Neglect air resistance.
 

Curvilinear Translation (Projectile Motion)

Projectile motion follows a parabolic trajectory. The vertical component of projectile is under constant gravitational acceleration and the horizontal component is at constant velocity. For easy handling, resolve the motion into x and y components and use the formulas in rectilinear translation.
 

Form the figure below:

$v_{ox} = v_o \, \cos \theta$

$v_{oy} = v_o \, \sin \theta$

 

000-projectile-general.gif