Moment of Inertia and Radius of Gyration
Moment of Inertia
Moment of inertia, also called the second moment of area, is the product of area and the square of its moment arm about a reference axis.
Moment of inertia about the x-axis:
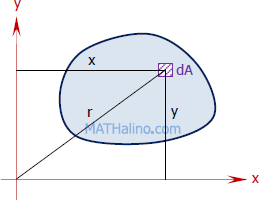
Moment of inertia about the y-axis:
Polar Moment of Inertia:
Polar moment of inertia is the moment of inertia about about the z-axis.
$\displaystyle J = \int r^2 \, dA$
Radius of Gyration
$k_x = \sqrt{\dfrac{I_x}{A}}$
$k_y = \sqrt{\dfrac{I_y}{A}}$
$k_z = \sqrt{\dfrac{J}{A}}$
Transfer Formula for Moment of Inertia
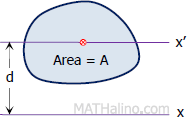
$x'$ = centroidal axis
$x$ = any axis parallel to the centroidal axis
$I$ = moment of inertia about the x-axis
$\bar{I}$ = centroidal moment of inertia
$A$ = area of the section
$d$ = distance between x and x’
In the same manner, the transfer formula for polar moment of inertia and the radii of gyration are respectively
$k^2 = {\bar{k}}^2 + d^2$
Product of Inertia
Moment of Inertia of Common Shapes
| Shape | Moment of Inertia | Radius of Gyration |
|---|---|---|
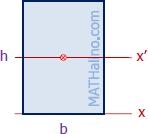
| Rectangle
|
$\bar{I}_x = \dfrac{bh^3}{12}$
$I_x = \dfrac{bh^3}{3}$ |
$\bar{k}_x = \dfrac{h}{\sqrt{12}}$
$k_x = \dfrac{h}{\sqrt{3}}$ |
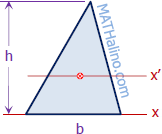
| Triangle
|
$\bar{I}_x = \dfrac{bh^3}{36}$
$I_x = \dfrac{bh^3}{12}$ |
$\bar{k}_x = \dfrac{h}{\sqrt{18}}$
$k_x = \dfrac{h}{\sqrt{6}}$ |
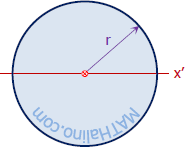
| Circle
|
$\bar{I}_x = \dfrac{\pi r^4}{4}$
$\bar{J} = \dfrac{\pi r^4}{2}$ |
$\bar{k}_x = \dfrac{r}{2}$
$\bar{k}_z = \dfrac{r}{\sqrt{2}}$ |
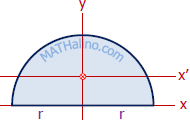
| Semicircle
|
$I_x = \bar{I}_y = \dfrac{\pi r^4}{8}$
$\bar{I}_x = 0.11r^4$ |
$k_x = \bar{k}_y = \dfrac{r}{2}$
$\bar{k}_x = 0.264r$ |
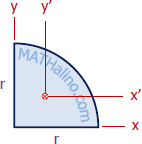
| Quarter circle
|
$I_x = I_y = \dfrac{\pi r^4}{16}$
$\bar{I}_x = \bar{I}_y = 0.055r^4$ |
$k_x = k_y = \dfrac{r}{2}$
$\bar{k}_x = \bar{k}_y = 0.264r$ |
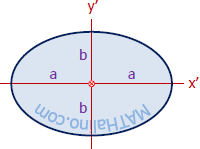
| Ellipse
|
$\bar{I}_x = \dfrac{\pi ab^3}{4}$
$\bar{I}_y = \dfrac{\pi a^3b}{4}$ |
$\bar{k}_x = \dfrac{b}{2}$
$\bar{k}_y = \dfrac{a}{2}$ |