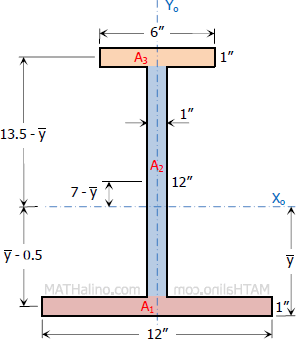
$A_1 = 12(1) = 12 \, \text{ in.}^2$
$y_1 = 0.5 \, \text{ in.}$
$\bar{I}_1 = \frac{1}{12}(12)(1^3) = 1 \, \text{ in.}^4$
$A_2 = 1(12) = 12 \, \text{ in.}^2$
$y_2 = 7 \, \text{ in.}$
$\bar{I}_2 = \frac{1}{12}(1)(12^3) = 144 \, \text{ in.}^4$
$A_3 = 6(1) = 6 \, \text{ in.}^2$
$y_3 = 13.5 \, \text{ in.}$
$\bar{I}_3 = \frac{1}{12}(6)(1^3) = 0.5 \, \text{ in.}^4$
$A\bar{y} = A_1y_1 + A_2y_2 + A_3y_3$
$30\bar{y} = 12(0.5) + 12(7) + 6(13.5)$
$\bar{y} = 5.7 \, \text{ in.}$
$\bar{I}_x = [ \, \bar{I}_1 + A_1(\bar{y} - 0.5)^2 \, ] + [ \, \bar{I}_2 + A_2(7 - \bar{y})^2 \, ] + [ \, \bar{I}_3 + A_3(13.5 - \bar{y})^2 \, ]$
$\bar{I}_x = [ \, 1 + 12(5.7 - 0.5)^2 \, ] + [ \, 144 + 12(7 - 5.7)^2 \, ] + [ \, 0.5 + 6(13.5 - 5.7)^2 \, ]$
$\bar{I}_x = 855.3 \, \text{ in.}^4$ answer
$\bar{I}_y = \frac{1}{12}(1)(12^3) + \frac{1}{12}(12)(1^3) + \frac{1}{12}(1)(6^3)$
$\bar{I}_y = 163 \, \text{ in.}^4$ answer
