Solution by Composite Areas
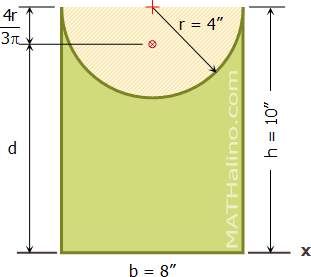
$I_{x-rectangle} = \dfrac{bh^3}{3} = \dfrac{8(10^3)}{3}$
$I_{x-rectangle} = 2666.67 ~ \text{in}^4$
By transfer formula for moment of inertia
$I = \bar{I} + Ad^2$
$I_{x-semicircle} = 0.11r^4 + Ad^2$
$I_{x-semicircle} = 0.11(4^4) + \frac{1}{2}\pi(4^2) \left[ 10 - \dfrac{4(4)}{3\pi} \right]^2$
$I_{x-semicircle} = 1760.53 ~ \text{in}^4$
Required moment of inertia
$I_x = I_{x-rectangle} - I_{x-semicircle}$
$I_x = 2666.67 - 1760.53$
$I_x = 906.14 ~ \text{in}^4$ answer
Solution by Integration
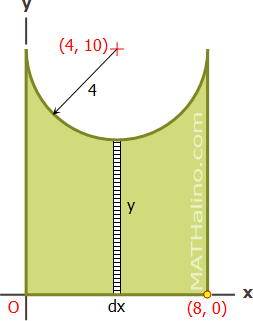$I_x = \dfrac{bh^3}{3}$
$\displaystyle I_x = \int_{x_1}^{x_2}\dfrac{(dx)(y^3)}{3}$
$\displaystyle I_x = \dfrac{1}{3}\int_0^8 y^3 \, dx$
Equation of the semi-circe with center at (h, k) = (4, 10) and radius, r = 4
$(x - h)^2 + (y - k)^2 = r^2$
$(x - 4)^2 + (y - 10)^2 = 4^2$
$(y - 10)^2 = 16 - (x - 4)^2$
$y - 10 = \pm \sqrt{16 - (x^2 - 8x + 16)}$
$y = \pm \sqrt{8x - x^2} + 10$
Use negative sign in the radical for the portion of the circle below y = 10
$y = 10 - \sqrt{8x - x^2}$
Thus,
$\displaystyle I_x = \dfrac{1}{3}\int_0^8 \left( 10 - \sqrt{8x - x^2} \right)^3 \, dx$
$I_x = \frac{1}{3}(2718.58)$
$I_x = 906.19 ~ \text{in}^4$ okay
