Properties of Wide Flange Sections
The technical content of this page is for educational purposes only and not intended for professional work.
- Read more about Properties of Wide Flange Sections
- Log in to post comments
moment of inertia
821 Rectangle minus semi-circle | Moment of Inertia
Problem 821
Find the moment of inertia about the indicated x-axis for the shaded area shown in Fig. P-821.
Area, moment of inertia, and radius of gyration of parabolic section
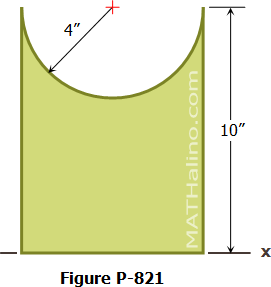
Situation
Given the parabola 3x2 + 40y – 4800 = 0.
Part 1: What is the area bounded by the parabola and the X-axis?
A. 6 200 unit2
B. 8 300 unit2
C. 5 600 unit2
D. 6 400 unit2
Part 2: What is the moment of inertia, about the X-axis, of the area bounded by the parabola and the X-axis?
A. 15 045 000 unit4
B. 18 362 000 unit4
C. 11 100 000 unit4
D. 21 065 000 unit4
Part 3: What is the radius of gyration, about the X-axis, of the area bounded by the parabola and the X-axis?
A. 57.4 units
B. 63.5 units
C. 47.5 units
D. 75.6 units
Problem 710 | Two simple beams at 90 degree to each other
Problem 710
Two timber beams are mounted at right angles and in contact with each other at their midpoints. The upper beam A is 2 in wide by 4 in deep and simply supported on an 8-ft span; the lower beam B is 3 in wide by 8 in deep and simply supported on a 10-ft span. At their cross-over point, they jointly support a load P = 2000 lb. Determine the contact force between the beams.
820 Unsymmetrical I-section | Moment of Inertia
Problem 820
Determine the moment of inertia of the area shown in Fig. P-819 with respect to its centroidal axes.
819 Inverted T-section | Moment of Inertia
Problem 819
Determine the moment of inertia of the T-section shown in Fig. P-819 with respect to its centroidal Xo axis.
- Read more about 819 Inverted T-section | Moment of Inertia
- Log in to post comments
818 Hollow square section | Moment of Inertia and Radius of Gyration
Problem 818
A hollow square cross section consists of an 8 in. by 8 in. square from which is subtracted a concentrically placed square 4 in. by 4 in. Find the polar moment of inertia and the polar radius of gyration with respect to a z axis passing through one of the outside corners.
817 Hollow Tube | Moment of Inertia and Radius of Gyration
Problem 817
Determine the moment of inertia and radius of gyration with respect to a polar centroidal axis of the cross section of a hollow tube whose outside diameter is 6 in. and inside diameter is 4 in.
816 Polar moment of inertia and radius of gyration at one corner of rectangle
Problem 816
A rectangle is 3 in. by 6 in. Determine the polar moment of inertia and the radius of gyration with respect to a polar axis through one corner.
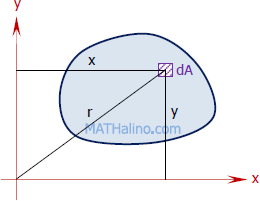
Moment of Inertia and Radius of Gyration
Moment of Inertia
Moment of inertia, also called the second moment of area, is the product of area and the square of its moment arm about a reference axis.
Moment of inertia about the x-axis:
$\displaystyle I_x = \int y^2 \, dA$
- Read more about Moment of Inertia and Radius of Gyration
- Log in to post comments