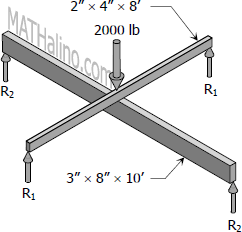
Let
R = contact force between beams A and B
Subscript (
A ) = for upper beam
Subscript (
B ) = for lower beam
Moment of inertia
$I_A = \dfrac{2(4^3)}{12} = \dfrac{32}{3} \, \text{ in}^4$
$I_B = \dfrac{3(8^3)}{12} = 128 \, \text{ in}^4$
Note:
The midspan deflection of a simple beam loaded with concentrated force at the midpoint is given by
$\delta = \dfrac{PL^3}{48EI}$
See Case No. 6 in the Summary of Beam Loadings.
The midspan of upper beam A is under 2000 lb applied load and contact force R. R will act upward at beam A.
$\delta_A = \dfrac{2000(8^3)(12^3)}{48E(\frac{32}{3})} - \dfrac{R(8^3)(12^3)}{48E(\frac{32}{3})}$
$\delta_A = \dfrac{3\,456\,000}{E} - \dfrac{1728R}{E}$
The lower beam B is subjected by the contact force R at midspan.
$\delta_B = \dfrac{R(10^3)(12^3)}{48E(128)}$
$\delta_B = \dfrac{1125R}{4E}$
The deflections of upper beam A and lower beam B are obviously equal. R will act downward at beam B.
$\delta_A = \delta_B$
$\dfrac{3\,456\,000}{E} - \dfrac{1728R}{E} = \dfrac{1125R}{4E}$
$3\,456\,000 = \dfrac{8037R}{4}$
$R = 1720.04 \, \text{ lb} \,$ answer
