midspan deflection
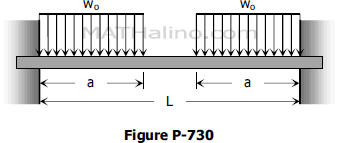
Problem 730 | Uniform loads at each end of fully restrained beam
Problem 703
Determine the end moment and maximum deflection for a perfectly restrained beam loaded as shown in Fig. P-730.
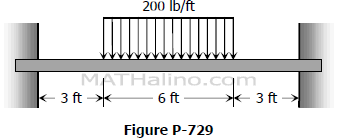
Problem 729 | Uniform load over the center part of fixed-ended beam
Problem 729
For the restrained beam shown in Fig. P-729, compute the end moment and maximum EIδ.
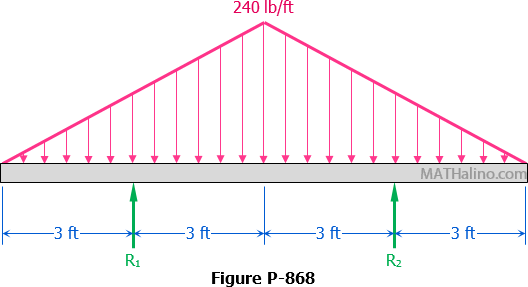
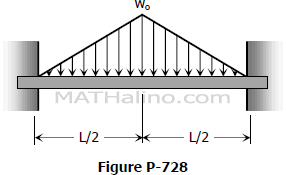
Problem 728 | Isosceles triangular load over the entire span of fully restrained beam
Problem 728
Determine the end moment and maximum deflection of a perfectly restrained beam loaded as shown in Fig. P-728.
Problem 727 | Fully restrained beam with uniform load over the entire span
Problem 727
Repeat Problem 726 assuming that the concentrated load is replaced by a uniformly distributed load of intensity wo over the entire length.
Problem 726 | Fully restrained beam with concentrated load at midspan
Problem 726
A beam of length L, perfectly restrained at both ends, supports a concentrated load P at midspan. Determine the end moment and maximum deflection.
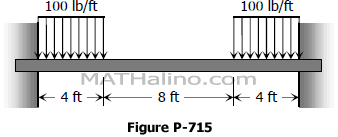
Problem 715 | Distributed loads placed symmetrically over fully restrained beam
Problem 12
Determine the moment and maximum EIδ for the restrained beam shown in Fig. RB-012. (Hint: Let the redundants be the shear and moment at the midspan. Also note that the midspan shear is zero.)
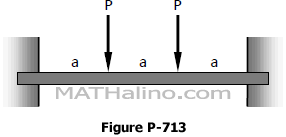
Problem 713 | Fully restrained beam with symmetrically placed concentrated loads
Problem 713
Determine the end moment and midspan value of EIδ for the restrained beam shown in Fig. PB-010. (Hint: Because of symmetry, the end shears are equal and the slope is zero at midspan. Let the redundant be the moment at midspan.)
Problem 710 | Two simple beams at 90 degree to each other
Problem 710
Two timber beams are mounted at right angles and in contact with each other at their midpoints. The upper beam A is 2 in wide by 4 in deep and simply supported on an 8-ft span; the lower beam B is 3 in wide by 8 in deep and simply supported on a 10-ft span. At their cross-over point, they jointly support a load P = 2000 lb. Determine the contact force between the beams.