midspan deflection

Problem 657
Determine the midspan value of EIδ for the beam shown in Fig. P-657.
 

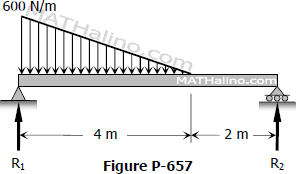
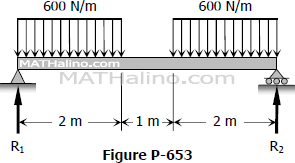
Problem 653
Compute the midspan value of EIδ for the beam shown in Fig. P-653. (Hint: Draw the M diagram by parts, starting from midspan toward the ends. Also take advantage of symmetry.
 

Problem 692
Find the value of EIδ midway between the supports for the beam shown in Fig. P-692. (Hint: Combine Case No. 11 and one half of Case No. 8.)
 

Problem 691
Determine the midspan deflection for the beam shown in Fig. P-691. (Hint: Apply Case No. 7 and integrate.)
 

Problem 690
The beam shown in Fig. P-690 has a rectangular cross section 50 mm wide. Determine the proper depth d of the beam if the midspan deflection of the beam is not to exceed 20 mm and the flexural stress is limited to 10 MPa. Use E = 10 GPa.
 

Problem 689
The beam shown in Fig. P-689 has a rectangular cross section 4 inches wide by 8 inches deep. Compute the value of P that will limit the midspan deflection to 0.5 inch. Use E = 1.5 × 10⁶ psi.

Problem 687
Determine the midspan deflection of the beam shown in Fig. P-687 if E = 10 GPa and I = 20 × 10⁶ mm⁴.
 

Problem 681
Show that the midspan value of EIδ is (w_ob/48)(L³ - 2Lb² + b³) for the beam in part (a) of Fig. P-681. Then use this result to find the midspan EIδ of the loading in part (b) by assuming the loading to exceed over two separate intervals that start from midspan and adding the results.
 

Problem 680
Determine the midspan value of EIδ for the beam loaded as shown in Fig. P-680.