Solution to Problem 691 | Beam Deflection by Method of Superposition

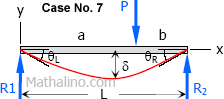
From Case No. 7, the midspan deflection is
 

$\delta = \dfrac{Pb}{48EI}(3L^2 - 4b^2) \text{ when } a \gt b$
 

For the given beam
 

$P = w_o dx$

$b = x$
 

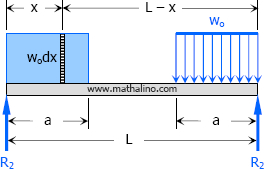$\displaystyle \delta = 2\int_0^a \dfrac{(w_odx)x}{48EI}(3L^2 - 4x^2)$

$\displaystyle \delta = \dfrac{w_o}{24EI}\int_0^a (3L^2x - 4x^3)dx$

$\displaystyle \delta = \dfrac{w_o}{24EI}\left[ \dfrac{3L^2x^2}{2} - x^4 \right]_0^a$

$\displaystyle \delta = \dfrac{w_o}{24EI}\left[ \dfrac{3L^2x^2 - 2x^4}{2} \right]_0^a$

$\displaystyle \delta = \dfrac{w_o}{48EI}\left[ 3L^2a^2 - 2a^4 \right]$

$\displaystyle \delta = \dfrac{w_oa^2}{48EI}(3L^2 - 2a^2)$           answer