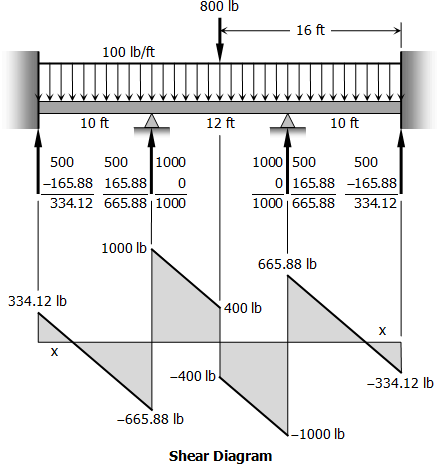
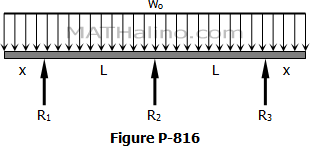
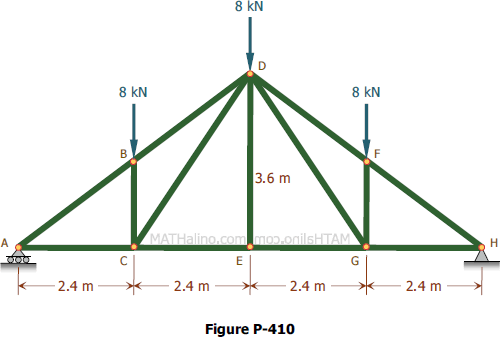
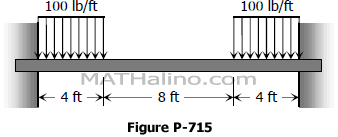
Support reactions of a symmetrically-loaded three-hinged arch structure
Situation
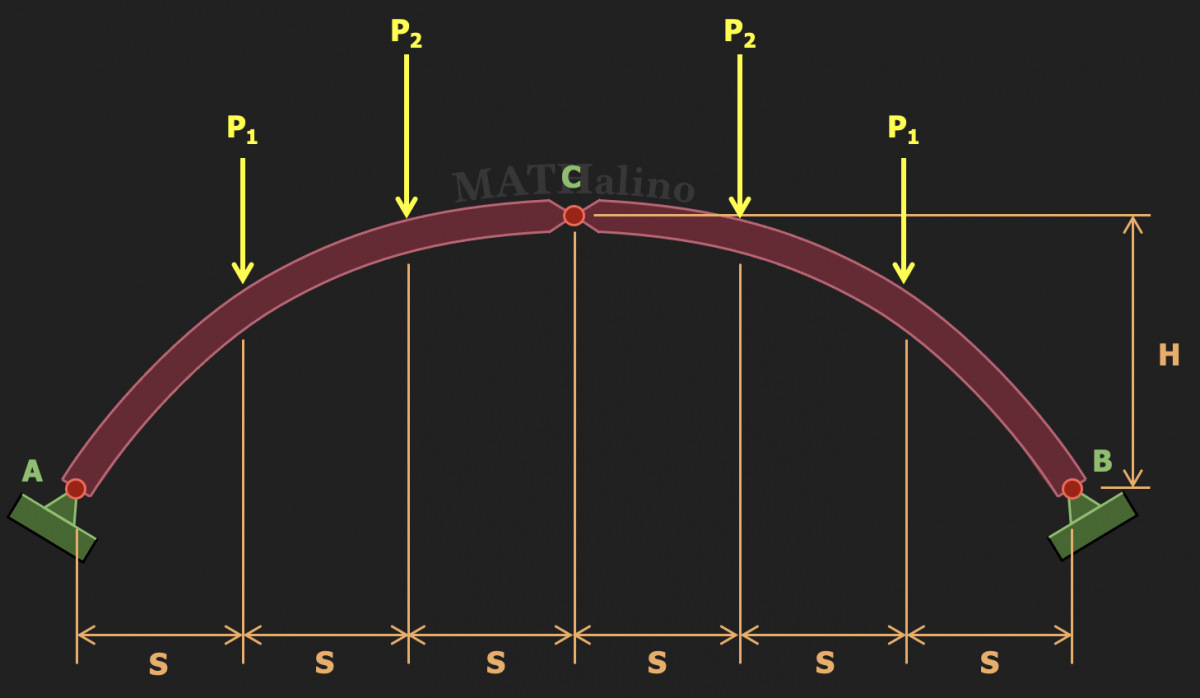
The three-hinged arch shown below is loaded with symmetrically placed concentrated loads as shown in the figure below.
The loads are as follows:
$$P_1 = 90 ~ \text{kN} \qquad P_2 = 240 ~ \text{kN}$$
The dimensions are:
$$H = 8 ~ \text{m} \qquad S = 4 ~ \text{kN}$$
Calculate the following:
1. The horizontal reaction at A.
| A. 0 | C. 330 kN |
| B. 285 kN | D. 436 kN |
2. The total reaction at B.
| A. 0 | C. 330 kN |
| B. 285 kN | D. 436 kN |
3. The vertical reaction at C.
| A. 0 | C. 330 kN |
| B. 285 kN | D. 436 kN |