Symmetrical Load

Problem 691
Determine the midspan deflection for the beam shown in Fig. P-691. (Hint: Apply Case No. 7 and integrate.)
 

Problem 674
Find the deflection midway between the supports for the overhanging beam shown in Fig. P-674.
 

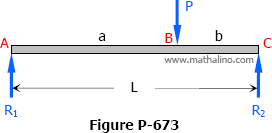
Problem 673
For the beam shown in Fig. P-673, show that the midspan deflection is δ = (Pb/48EI) (3L² - 4b²).
 

In simply supported beams, the tangent drawn to the elastic curve at the point of maximum deflection is horizontal and parallel to the unloaded beam. It simply means that the deviation from unsettling supports to the horizontal tangent is equal to the maximum deflection. If the simple beam is symmetrically loaded, the maximum deflection will occur at the midspan.
 

Problem 663
Determine the maximum deflection of the beam carrying a uniformly distributed load over the middle portion, as shown in Fig. P-663. Check your answer by letting 2b = L.
 

Problem 662
Determine the maximum deflection of the beam shown in Fig. P-662. Check your result by letting a = L/2 and comparing with case 8 in Table 6-2. Also, use your result to check the answer to Prob. 653.
 

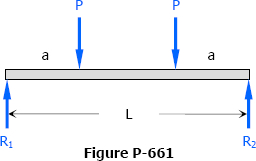
Problem 661
Compute the midspan deflection of the symmetrically loaded beam shown in Fig. P-661. Check your answer by letting a = L/2 and comparing with the answer to Problem 609.
 

Problem 626
For the beam loaded as shown in Fig. P-626, compute the moment of area of the M diagrams between the reactions about both the left and the right reaction.
 

Problem 620
Find the midspan deflection δ for the beam shown in Fig. P-620, carrying two triangularly distributed loads. (Hint: For convenience, select the origin of the axes at the midspan position of the elastic curve.)
 

Problem 609
As shown in Fig. P-609, a simply supported beam carries two symmetrically placed concentrated loads. Compute the maximum deflection δ.