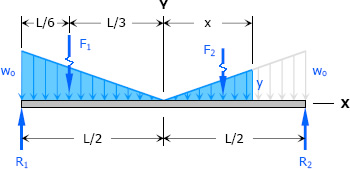
By ratio and proportion:
$\dfrac{y}{x} = \dfrac{w_o}{L/2}$
$y = \dfrac{2w_o}{L}x$
By symmetry:
$R_1 = R_2 = \frac{1}{2}(L/2)(w_o) = \frac{1}{4}w_oL$
$F_1 = \frac{1}{2}(L/2)(w_o) = \frac{1}{4}w_oL$
$F_2 = \frac{1}{2} xy = \frac{1}{2}x \left( \dfrac{2w_o}{L}x \right) = \dfrac{w_o}{L}x^2$
$EI \, y'' = R_1(x + \frac{1}{2}L) - F_1(x + \frac{1}{3}L) - F_2(\frac{1}{3}x)$
$EI \, y'' = \frac{1}{4}w_oL(x + \frac{1}{2}L) - \frac{1}{4}w_oL(x + \frac{1}{3}L) - \dfrac{w_o}{L}x^2(\frac{1}{3}x)$
$EI \, y'' = \frac{1}{4}w_oLx + \frac{1}{8}w_oL^2 - \frac{1}{4}w_oLx - \frac{1}{12}w_oL^2 - \dfrac{w_o}{3L}x^3$
$EI \, y'' = \frac{1}{24}w_oL^2 - \dfrac{w_o}{3L}x^3$
$EI \, y' = \frac{1}{24}w_oL^2x - \dfrac{w_o}{12L}x^4 + C_1$
$EI \, y = \frac{1}{48}w_oL^2x^2 - \dfrac{w_o}{60L}x^5 + C_1x + C_2$
At x = 0, y' = 0, therefore C1 = 0
At x = ½L, y = 0
0 = (1/48)woL2 (½L)2 - (wo60L)(½L)5 + C2
0 = (1/192)wo L4 - (1/1920)wo L4 + C2
C2 = -(3/640)wo L4
Therefore,
$EI \, y = \frac{1}{48}w_oL^2x^2 - \dfrac{w_o}{60L}x^5 - \frac{3}{640}w_o L^4$
At x = 0 (midspan)
$EI \, y_{max} = -\frac{3}{640}w_o L^4 = -\frac{3}{640}w_o L^4 \times \frac{3}{3}$
$EI \, y_{max} = -\frac{9}{1920}w_o L^4$
Thus,
$\delta_{midspan} = \dfrac{9w_oL^4}{1920EI}$ answer
