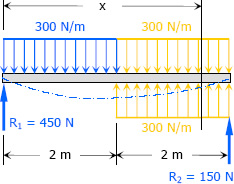
$\Sigma M_{R2} = 0$
$4R_1 = 300(2)(3)$
$R_1 = 450 \, \text{N}$
$\Sigma M_{R1} = 0$
$4R_2 = 300(2)(1)$
$R_2 = 150 \, \text{N}$
$EI \, y'' = 450x - 300x \cdot \frac{1}{2}x + 300 \langle \, x - 2 \, \rangle \cdot \frac{1}{2}\langle \, x - 2 \, \rangle$
$EI \, y'' = 450x - 150x^2 + 150\langle \, x - 2 \, \rangle^2$
$EI \, y' = 225x^2 - 50x^3 + 50 \langle \, x - 2 \, \rangle^3 + C_1$
$EI \, y = 75x^3 - 12.5x^4 + 12.5 \langle \, x - 2 \, \rangle^4 + C_1x + C_2$
At x = 0, y = 0, therefore C2 = 0
At x = 4 m, y = 0
$0 = 75(4^3) - 12.5(4^4) + 12.5(4 - 2)^4 + 4C_1$
$C_1 = -450 \, \text{N}\cdot\text{m}^2$
Therefore,
$EI \, y = 75x^3 - 12.5x^4 + 12.5 \langle \, x - 2 \, \rangle^4 - 450x$
At x = 2 m (midspan)
$EI \, y_{midspan} = 75(2^3) - 12.5(2^4) + 12.5(2 - 2)^4 - 450(2)$
$EI \, y_{midspan} = -500 \, \text{N}\cdot\text{m}^3$
$EI \, \delta_{midspan} = 500 \, \text{N}\cdot\text{m}^3$
Maximum midspan deflection
$\delta_{midspan} = \frac{1}{360}L = \frac{1}{360}(4) = \frac{1}{90} \, \text{m}$
$\delta_{midspan} = \frac{100}{9} \, \text{mm}$
Thus,
$10\,000I \, ( \frac{100}{9} ) = 500(1000^3)$
$I = 4\,500\,000 \, \text{mm}^4$
$I = 4.5 \times 10^6 \, \text{mm}^4$ answer
