Solution to Problem 616 | Double Integration Method

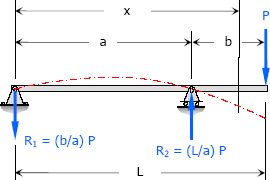
$\Sigma M_{R2} = 0 $

$aR_1 = bP $

$R_1 = \dfrac{b}{a}P $
 

$\Sigma M_{R1} = 0$

$aR_2 = PL$

$R_2 = \dfrac{L}{a}P$
 

$EI \, y'' = -\dfrac{b}{a}Px + \dfrac{L}{a}P \, \langle \, x - a \, \rangle$

$EI \, y' = -\dfrac{b}{2a}Px^2 + \dfrac{L}{2a}P \, \langle \, x - a \, \rangle^2 + C_1$

$EI \, y = -\dfrac{b}{6a}Px^3 + \dfrac{L}{6a}P \, \langle \, x - a \, \rangle^3 + C_1x + C_2$
 

At x = 0, y = 0, therefore C₂ = 0

At x = a, y = 0
0 = -[ b / (6a) ] Pa³ + aC₁
C₁ = (ab/6)P
 

Therefore,
$EI \, y' = -\dfrac{b}{2a}Px^2 + \dfrac{L}{2a}P \, \langle \, x - a \, \rangle^2 + \dfrac{ab}{6}P$

$EI \, y = -\dfrac{b}{6a}Px^3 + \dfrac{L}{6a}P \, \langle \, x - a \, \rangle^3 + \dfrac{ab}{6}Px$
 

Part (a): Slope and deflection under the load P

 

Slope under the load P: (note x = a + b = L)

$EI \, y' = -\dfrac{b}{2a}P(a + b)^2 + \dfrac{a + b}{2a}Pb^2 + \dfrac{ab}{6}P$

$EI \, y' = -\dfrac{b}{2a}P(a^2 + 2ab + b^2) + \dfrac{ab^2 + b^3}{2a}P + \dfrac{ab}{6}P$

$EI \, y' = -\dfrac{ab}{2}P - b^2P - \dfrac{b^3}{2a}P + \dfrac{b^2}{2}P \dfrac{b^3}{2a}P + \dfrac{ab}{6}P$

$EI \, y' = -\frac{1}{2}b^2P - \frac{1}{3}abP$

$EI y' = - \frac{1}{6}b \, (3b + 2a)P$

$EI y' = - \frac{1}{6}b \, [ \, 2(a + b) + b \, ] P$

$EI y' = - \frac{1}{6}b \, (2L + b)P$           answer

 

Deflection under the load P: (note x = a + b = L)

$EI \, y = -\dfrac{b}{6a}P(a + b)^3 + \dfrac{a + b}{6a}P(b^3) + \dfrac{ab}{6}P(a + b)$

$EI \, y = -\dfrac{b}{6a}P(a^3 + 3a^2b + 3ab^2 + b^3) + \dfrac{ab^3 + b^4}{6a}P + \dfrac{ab}{6}P(a + b)$

$EI \, y = -\dfrac{a^2b}{6}P - \dfrac{ab^2}{2}P - \dfrac{b^3}{2}P - \dfrac{b^4}{6a}P + \dfrac{b^3}{6}P + \dfrac{b^4}{6a}P + \dfrac{a^2b}{6}P + \dfrac{ab^2}{6}P$

$EI \, y = -\frac{1}{3}ab^2P - \frac{1}{3}b^3P$

$EI \, y = -\frac{1}{3}(a + b) \, b^2P$

$EI \, y = -\frac{1}{3}Lb^2P$           answer

 

Part (b): Maximum deflection between the supports

 

The maximum deflection between the supports will occur at the point where y' = 0.

$EI \, y' = -\dfrac{b}{2a}Px^2 + \dfrac{L}{2a}P \, \langle \, x - a \, \rangle^2 + \dfrac{ab}{6}P$
 

At y' = 0, ⟨ x - a ⟩ do not exist thus,

$0 = -\dfrac{b}{2a}Px^2 + \dfrac{ab}{6}P$

$x^2 = \frac{1}{3}a^2$

$x = \frac{1}{\sqrt{3}}a$
 

At $x = \frac{1}{\sqrt{3}}a$,

$EI \, y_{max} = -\dfrac{b}{6a}P(\frac{1}{\sqrt{3}}a)^3 + \dfrac{ab}{6}P(\frac{1}{\sqrt{3}}a)$

$EI \, y_{max} = -\dfrac{a^2b}{6(3\sqrt{3})}P + \dfrac{a^2b}{6\sqrt{3}}P$

$EI \, y_{max} = \dfrac{a^2b}{6\sqrt{3}}P \, \left( -\dfrac{1}{3} + 1 \right)$

$EI \, y_{max} = \dfrac{a^2b}{6\sqrt{3}}P \, \left( \dfrac{2}{3} \right)$

$EI \, y_{max} = \dfrac{a^2b}{9\sqrt{3}}P$           answer