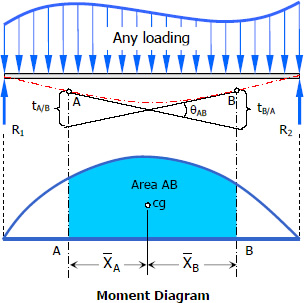
Method of Superposition | Beam Deflection
The slope or deflection at any point on the beam is equal to the resultant of the slopes or deflections at that point caused by each of the load acting separately.
- Read more about Method of Superposition | Beam Deflection
- Log in to post comments