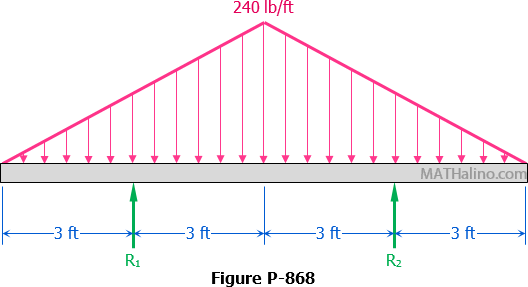
Simply Supported Beam with Support Added at Midspan to Prevent Excessive Deflection
Situation
A simply supported beam has a span of 12 m. The beam carries a total uniformly distributed load of 21.5 kN/m.
1. To prevent excessive deflection, a support is added at midspan. Calculate the resulting moment (kN·m) at the added support.
| A. 64.5 | C. 258.0 |
| B. 96.8 | D. 86.0 |
2. Calculate the resulting maximum positive moment (kN·m) when a support is added at midspan.
| A. 96.75 | C. 108.84 |
| B. 54.42 | D. 77.40 |
3. Calculate the reaction (kN) at the added support.
| A. 48.38 | C. 161.2 |
| B. 96.75 | D. 80.62 |