Solution to Problem 693 | Beam Deflection by Method of Superposition
Problem 693
Determine the value of EIδ at the left end of the overhanging beam in Fig. P-693.
Solution to Problem 689 | Beam Deflection by Method of Superposition
Problem 689
The beam shown in Fig. P-689 has a rectangular cross section 4 inches wide by 8 inches deep. Compute the value of P that will limit the midspan deflection to 0.5 inch. Use E = 1.5 × 106 psi.
Solution to Problem 688 | Beam Deflection by Method of Superposition
Problem 688
Determine the midspan value of EIδ at the left end of the beam shown in Fig. P-688.
Solution to Problem 686 | Beam Deflection by Method of Superposition
Problem 686
Determine the value of EIδ under each concentrated load in Fig. P-686.
Solution to Problem 675 | Midspan Deflection
Problem 675
Repeat Prob. 674 for the overhanging beam shown in Fig. P-675.
- Read more about Solution to Problem 675 | Midspan Deflection
- Log in or register to post comments
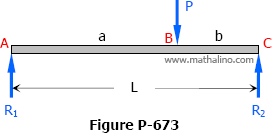
Solution to Problem 673 | Midspan Deflection
Problem 673
For the beam shown in Fig. P-673, show that the midspan deflection is δ = (Pb/48EI) (3L2 - 4b2).
- Read more about Solution to Problem 673 | Midspan Deflection
- Log in or register to post comments
Solution to Problem 670 | Deflections in Simply Supported Beams
Problem 670
Determine the value of EIδ at the left end of the overhanging beam shown in Fig. P-670.
Solution to Problem 669 | Deflections in Simply Supported Beams
Problem 669
Compute the value of EIδ midway between the supports of the beam shown in Fig. P-669.
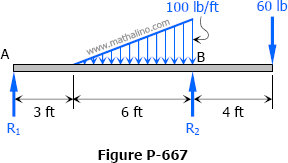
Solution to Problem 668 | Deflections in Simply Supported Beams
Problem 668
For the beam shown in Fig. P-668, compute the value of P that will cause the tangent to the elastic curve over support R2 to be horizontal. What will then be the value of EIδ under the 100-lb load?
Solution to Problem 667 | Deflections in Simply Supported Beams
Problem 667
Determine the value of EIδ at the right end of the overhanging beam shown in Fig. P-667. Is the deflection up or down?
