Solution to Problem 675 | Midspan Deflection

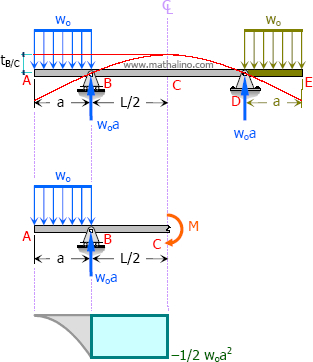
$M = w_oa (\frac{1}{2}L) - w_oa (\frac{1}{2}L + \frac{1}{2}a)$

$M = \frac{1}{2}w_oLa - \frac{1}{2}w_oLa - \frac{1}{2}w_oa^2$

$M = -\frac{1}{2}w_oa^2$
 

$EI \, t_{B/C} = (Area_{BC}) \, \bar{X}_B$

$EI \, t_{B/C} = \frac{1}{2}L(-\frac{1}{2}w_oa^2)(\frac{1}{4}L)$

$EI \, t_{B/C} = -\frac{1}{16}w_oL^2a^2$

$t_{B/C} = -\dfrac{1}{16EI}w_oL^2a^2$
 

$2\delta = t_{B/C}$

$2\delta = -\dfrac{1}{16EI}w_oL^2a^2$

$\delta = -\dfrac{1}{32EI}w_oL^2a^2$

$\delta = \dfrac{1}{32EI}w_oL^2a^2 \, \text{ upward}$           answer