rectangular load
Problem 822 | Continuous Beam by Three-Moment Equation
Problem 822
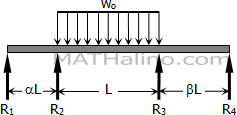
Solve Prob. 821 if the concentrated load is replaced by a uniformly distributed load of intensity wo over the middle span.
Answers:
$M_2 = -\dfrac{w_o L^2}{4} \cdot \dfrac{1 + 2\beta}{4(\alpha + 1)(1 + \beta) - 1}$
$M_3 = -\dfrac{w_o L^2}{4} \cdot \dfrac{1 + 2\alpha}{4(1 + \alpha)(1 + \beta) - 1}$
Problem 820 | Continuous Beam by Three-Moment Equation
Problem 820
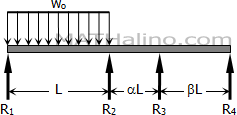
Solve Prob. 819 if the concentrated load is replaced by a uniformly distributed load of intensity wo over the first span.
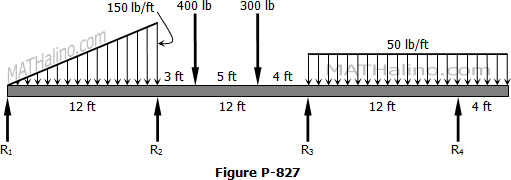
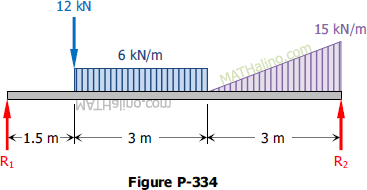
Problem 334 | Equilibrium of Parallel Force System
Problem 334
Determine the reactions for the beam loaded as shown in Fig. P-334.
Solution to Problem 691 | Beam Deflection by Method of Superposition
Problem 691
Determine the midspan deflection for the beam shown in Fig. P-691. (Hint: Apply Case No. 7 and integrate.)
Solution to Problem 689 | Beam Deflection by Method of Superposition
Problem 689
The beam shown in Fig. P-689 has a rectangular cross section 4 inches wide by 8 inches deep. Compute the value of P that will limit the midspan deflection to 0.5 inch. Use E = 1.5 × 106 psi.
Solution to Problem 687 | Beam Deflection by Method of Superposition
Problem 687
Determine the midspan deflection of the beam shown in Fig. P-687 if E = 10 GPa and I = 20 × 106 mm4.