rectangular load

Problem 681
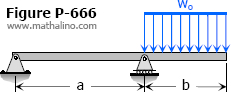
Show that the midspan value of EIδ is (w_ob/48)(L³ - 2Lb² + b³) for the beam in part (a) of Fig. P-681. Then use this result to find the midspan EIδ of the loading in part (b) by assuming the loading to exceed over two separate intervals that start from midspan and adding the results.
 

Problem 675
Repeat Prob. 674 for the overhanging beam shown in Fig. P-675.
 

Problem 666
Determine the value of EIδ at the right end of the overhanging beam shown in Fig. P-666.
 

Problem 665
Replace the concentrated load in Prob. 664 by a uniformly distributed load of intensity w_o acting over the middle half of the beam. Find the maximum deflection.
 

Coplanar Parallel Force System
Parallel forces can be in the same or in opposite directions. The sign of the direction can be chosen arbitrarily, meaning, taking one direction as positive makes the opposite direction negative. The complete definition of the resultant is according to its magnitude, direction, and line of action.
 

Problem 632
For the beam loaded as shown in Fig. P-632, compute the value of (Area_AB) barred(X)_A. From this result, is the tangent drawn to the elastic curve at B directed up or down to the right? (Hint: Refer to the deviation equations and rules of sign.)
 

Problem 631
Determine the value of the couple M for the beam loaded as shown in Fig. P-631 so that the moment of area about A of the M diagram between A and B will be zero. What is the physical significance of this result?