Three-moment equation between spans (1) and (2)
$M_1 L_1 + 2M_2(L_1 + L_2) + M_3 L_2 + \dfrac{6A_1\bar{a}_1}{L_1} + \dfrac{6A_2\bar{b}_2}{L_2} = 0$
Where,
$M_1 = 0$
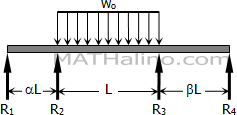
$L_1 = \alpha L$
$L_2 = L$
$\dfrac{6A_1\bar{a}_1}{L_1} = 0$
$\dfrac{6A_2\bar{b}_2}{L_2} = \frac{1}{4}w_o L^3$
Thus,
$0 + 2M_2(\alpha L + L) + M_3L + 0 + \frac{1}{4}w_o L^3 = 0$
$2M_2(\alpha + 1)L + M_3L + \frac{1}{4}w_o L^3 = 0$
$2M_2(\alpha + 1) + M_3 + \frac{1}{4}w_o L^2 = 0$
$M_3 = -\frac{1}{4}w_o L^2 - 2M_2(\alpha + 1)$ ← equation (1)
Three-moment equation between spans (2) and (3)
$M_2 L_2 + 2M_3(L_2 + L_3) + M_4 L_3 + \dfrac{6A_2\bar{a}_2}{L_2} + \dfrac{6A_3\bar{b}_3}{L_3} = 0$
Where,
$L_2 = L$
$L_3 = \beta L$
$M_4 = 0$
$\dfrac{6A_2\bar{a}_2}{L_2} = \frac{1}{4}w_o L^3$
$\dfrac{6A_3\bar{b}_3}{L_3} = 0$
Thus,
$M_2 L + 2M_3(L + \beta L) + 0 + \frac{1}{4}w_o L^3 + 0 = 0$
$M_2 L + 2M_3(1 + \beta)L + \frac{1}{4}w_o L^3 = 0$
$M_2 + 2M_3(1 + \beta) + \frac{1}{4}w_o L^2 = 0$
$M_2 + 2(1 + \beta)M_3 = -\frac{1}{4}w_o L^2$
$M_2 + 2(1 + \beta)[ \, -\frac{1}{4}w_o L^2 - 2M_2(\alpha + 1) \, ] = -\frac{1}{4}w_o L^2$
$M_2 - 2(1 + \beta)(\frac{1}{4}w_o L^2) - 4(\alpha + 1)(1 + \beta)M_2 = -\frac{1}{4}w_o L^2$
$M_2 - 4(\alpha + 1)(1 + \beta)M_2 = -\frac{1}{4}w_o L^2 + 2(1 + \beta)(\frac{1}{4}w_o L^2)$
$[ \, 1 - 4(\alpha + 1)(1 + \beta) \, ] M_2 = -\frac{1}{4}w_o L^2 [ \, 1 - 2(1 + \beta) \, ]$
$M_2 = -\dfrac{w_o L^2}{4} \cdot \dfrac{1 - 2(1 + \beta)}{1 - 4(\alpha + 1)(1 + \beta)}$
$M_2 = -\dfrac{w_o L^2}{4} \cdot \dfrac{1 - 2 - 2\beta}{1 - 4(\alpha + 1)(1 + \beta)}$
$M_2 = -\dfrac{w_o L^2}{4} \cdot \dfrac{-1 - 2\beta}{1 - 4(\alpha + 1)(1 + \beta)}$
$M_2 = -\dfrac{w_o L^2}{4} \cdot \dfrac{-(1 + 2\beta)}{1 - 4(\alpha + 1)(1 + \beta)}$
$M_2 = -\dfrac{w_o L^2}{4} \cdot \dfrac{1 + 2\beta}{4(\alpha + 1)(1 + \beta) - 1}$ answer
From equation (1)
$M_3 = -\frac{1}{4}w_o L^2 - 2 \left[ -\dfrac{w_o L^2}{4} \cdot \dfrac{1 + 2\beta}{4(\alpha + 1)(1 + \beta) - 1} \right] (\alpha + 1)$
$M_3 = -\dfrac{w_o L^2}{4} + \dfrac{w_o L^2}{4} \cdot \dfrac{2(1 + 2\beta)(\alpha + 1)}{4(\alpha + 1)(1 + \beta) - 1}$
$M_3 = -\dfrac{w_o L^2}{4} \left[ 1 - \dfrac{2(1 + 2\beta)(\alpha + 1)}{4(\alpha + 1)(1 + \beta) - 1} \right]$
$M_3 = -\dfrac{w_o L^2}{4} \left[ \dfrac{4(\alpha + 1)(1 + \beta) - 1 - 2(1 + 2\beta)(\alpha + 1)}{4(\alpha + 1)(1 + \beta) - 1} \right]$
$M_3 = -\dfrac{w_o L^2}{4} \left[ \dfrac{4(\alpha + \alpha \beta + 1 + \beta) - 1 - 2(\alpha + 1 + 2\alpha \beta + 2\beta)}{4(\alpha + 1)(1 + \beta) - 1} \right]$
$M_3 = -\dfrac{w_o L^2}{4} \left[ \dfrac{4\alpha + 4\alpha \beta + 4 + 4\beta - 1 - 2\alpha - 2 - 4\alpha \beta - 4\beta}{4(1 + \alpha)(1 + \beta) - 1} \right]$
$M_3 = -\dfrac{w_o L^2}{4} \left[ \dfrac{2\alpha + 1}{4(1 + \alpha)(1 + \beta) - 1} \right]$
$M_3 = -\dfrac{w_o L^2}{4} \cdot \dfrac{1 + 2\alpha}{4(1 + \alpha)(1 + \beta) - 1}$ answer
