$M_1L_1 + 2M_2(L_1 + L_2) + M_3L_2 + \dfrac{6A_1\bar{a}_1}{L_1} + \dfrac{6A_2\bar{b}_2}{L_2} = 0$
Where
$L_1 = L_2 = 9 ~ \text{ft}$
$M_1 = M_3 = 0$
$\dfrac{6A_1\bar{a}_1}{L_1} = -\dfrac{M}{L}(3a^2 - L^2) = -\dfrac{300}{9}[ \, 3(3^2) - 9^2 \, ]$
$\dfrac{6A_1\bar{a}_1}{L_1} = 1800 ~ \text{lb}\cdot\text{ft}$
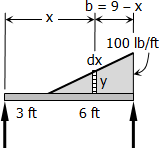$\dfrac{y}{x - 3} = \dfrac{100}{6}$
$y = \frac{50}{3}(x - 3)$
$P = y \, dx = \frac{50}{3}(x - 3) \, dx$
$\dfrac{6A_2\bar{b}_2}{L_2} = \dfrac{Pb}{L}(L^2 - b^2)$
$\displaystyle \dfrac{6A_2\bar{b}_2}{L_2} = {\int_3^9} \dfrac{[ \, \frac{50}{3}(x - 3) \, dx \, ](9 - x)}{9} [ \, 9^2 - (9 - x)^2 \, ]$
$\displaystyle \dfrac{6A_2\bar{b}_2}{L_2} = \dfrac{50}{27}{\int_3^9} (x - 3)(9 - x)[ \, 81 - (81 - 18x + x^2) \, ] \, dx$
$\displaystyle \dfrac{6A_2\bar{b}_2}{L_2} = \dfrac{50}{27}{\int_3^9} (x - 3)(9 - x)(18x - x^2) \, dx$
$\dfrac{6A_2\bar{b}_2}{L_2} = 4680 ~ \text{lb}\cdot\text{ft}^2$
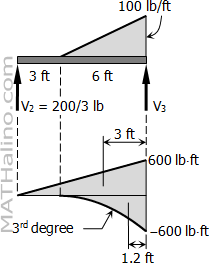Another way to solve for $\dfrac{6A_2\bar{b}_2}{L_2}$
$\Sigma M_{V3} = 0$
$9V_2 = \frac{1}{2}(6)(100)[ \, \frac{1}{3}(6) \, ]$
$V_2 = \frac{200}{3} ~ \text{lb}$
$\dfrac{6A_2\bar{b}_2}{L_2} = \frac{6}{9} [ \, \frac{1}{2}(9)(600)(3) - \frac{1}{4}(6)(600)(1.2) \, ]$
$\dfrac{6A_2\bar{b}_2}{L_2} = 4680 ~ \text{lb}\cdot\text{ft}^2$
Thus,
$0 + 2M_2(9 + 9) + 0 + 1800 + 4680 = 0$
$36M_2 = -6480$
$M_2 = -180 ~ \text{lb}\cdot\text{ft}$ answer
