Apply three-moment equation to spans (1) and (2)
$M_1 L_1 + 2M_2(L_1 + L_2) + M_3 L_2 + \dfrac{6A_1\bar{a}_1}{L_1} + \dfrac{6A_2\bar{b}_2}{L_2} = 0$
Where,
$M_1 = 0$
$L_1 = 4 ~ \text{m}$
$L_2 = 2 ~ \text{m}$
$\dfrac{6A_1\bar{a}_1}{L_1} = \frac{1}{4}w_oL^3 = \frac{1}{4}(2)(4^3) = 32 ~ \text{kN}\cdot\text{m}^2$
$\dfrac{6A_2\bar{b}_2}{L_2} = \frac{3}{8}PL^2 = \frac{3}{8}(10)(2^2) = 15 ~ \text{kN}\cdot\text{m}^2$
Thus,
$0 + 2M_2(4 + 2) + M_3(2) + 32 + 15 = 0$
$12M2 + 2M3 = -47$ &right; equation (1)
Apply three-moment equation to spans (2) and (3)
$M_2 L_2 + 2M_3(L_2 + L_3) + M_4 L_3 + \dfrac{6A_2\bar{a}_2}{L_2} + \dfrac{6A_3\bar{b}_3}{L_3} = 0$
Where,
$L_2 = 2 ~ \text{m}$
$L_3 = 4 ~ \text{m}$
$M_4 = 0$
$\dfrac{6A_2\bar{a}_2}{L_2} = \frac{3}{8}PL^2 = \frac{3}{8}(10)(2^2) = 15 ~ \text{kN}\cdot\text{m}^2$
$\dfrac{6A_3\bar{b}_3}{L_3} = \frac{1}{4}w_oL^3 = \frac{1}{4}(4)(4^3) = 64 ~ \text{kN}\cdot\text{m}^2$
Thus,
$M_2(2) + 2M_3(2 + 4) + 0 + 15 + 64 = 0$
$2M_2 + 12M_3 = -79$ &right; equation (2)
From equations (1) and (2)
$M_2 = -2.9 ~ \text{kN}\cdot\text{m}$ answer
$M_3 = -6.1 ~ \text{kN}\cdot\text{m}$ answer
Checking:
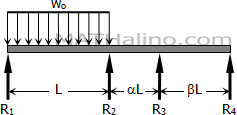From Solution 820
$M_2 = -\dfrac{w_o L^2}{4} \cdot \dfrac{2(\alpha + \beta)}{4(1 + \alpha)(\alpha + \beta) - \alpha^2}$
$M_3 = \dfrac{w_o L^2}{4} \cdot \dfrac{\alpha}{4(1 + \alpha)(\alpha + \beta) - \alpha^2}$
For the first span of this problem:
α = 0.5, β = 1, L = 4 m, and wo = 2 kN/m
$M_2 = -\dfrac{2(4^2)}{4} \cdot \dfrac{2(0.5 + 1)}{4(1 + 0.5)(0.5 + 1) - 0.5^2} = -\frac{96}{35} ~ \text{kN}\cdot\text{m}$
$M_3 = \dfrac{2(4^2)}{4} \cdot \dfrac{0.5}{4(1 + 0.5)(0.5 + 1) - 0.5^2} = \frac{16}{35} ~ \text{kN}\cdot\text{m}$
For the third span of this problem:
α = 0.5, β = 1, L = 4 m, and wo = 4 kN/m
$M_3 = -\dfrac{4(4^2)}{4} \cdot \dfrac{2(0.5 + 1)}{4(1 + 0.5)(0.5 + 1) - 0.5^2} = -\frac{192}{35} ~ \text{kN}\cdot\text{m}$
$M_2 = \dfrac{4(4^2)}{4} \cdot \dfrac{0.5}{4(1 + 0.5)(0.5 + 1) - 0.5^2} = \frac{32}{35} ~ \text{kN}\cdot\text{m}$
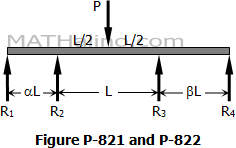From Solution 821
$M_2 = -\dfrac{3PL}{8} \cdot \dfrac{1 + 2\beta}{4(1 + \alpha)(1 + \beta) - 1}$
$M_3 = -\dfrac{3PL}{8} \cdot \dfrac{1 + 2\alpha}{4(1 + \alpha)(1 + \beta) - 1}$
For the middle span of this problem:
α = β = 2, L = 2 m, and P = 10 kN
$M_2 = -\dfrac{3(10)(2)}{8} \cdot \dfrac{1 + 2(2)}{4(1 + 2)(1 + 2) - 1} = -\frac{15}{14} ~ \text{kN}\cdot\text{m}$
$M_3 = -\dfrac{3(10)(2)}{8} \cdot \dfrac{1 + 2(2)}{4(1 + 2)(1 + 2) - 1} = -\frac{15}{14} ~ \text{kN}\cdot\text{m}$
Thus,
$M_2 = -\frac{96}{35} + \frac{32}{35} - \frac{15}{14} = -2.9 ~ \text{kN}\cdot\text{m}$ answer
$M_3 = \frac{16}{35} - \frac{192}{35} - \frac{15}{14} = -6.1 ~ \text{kN}\cdot\text{m}$ answer
