The Three-Moment Equation

The three-moment equation gives us the relation between the moments between any three points in a beam and their relative vertical distances or deviations. This method is widely used in finding the reactions in a continuous beam.

Consider three points on the beam loaded as shown.

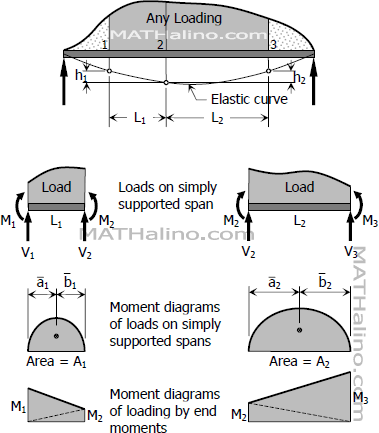
From proportions between similar triangles:
$\dfrac{h_1 - t_{1/2}}{L_1} = \dfrac{t_{3/2} - h_3}{L_2}$

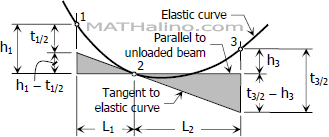
$\dfrac{h_1}{L_1} - \dfrac{t_{1/2}}{L_1} = \dfrac{t_{3/2}}{L_2} - \dfrac{h_3}{L_2}$

$\dfrac{t_{1/2}}{L_1} + \dfrac{t_{3/2}}{L_2} = \dfrac{h_1}{L_1} + \dfrac{h_3}{L_2}$ → equation (1)

Values of t_1/2 and t_3/2
$t_{1/2} = \dfrac{1}{E_1I_1}(\text{Area}_{1-2})\cdot\bar{X}_1$

$t_{1/2} = \dfrac{1}{E_1I_1}\left[ A_1\bar{a}_1 + (\frac{1}{2}M_1L_1)(\frac{1}{3}L_1) + (\frac{1}{2}M_2L_1)(\frac{2}{3}L_1) \right]$

$t_{1/2} = \dfrac{1}{6E_1I_1}(6A_1\bar{a}_1 + M_1{L_1}^2 + 2M_2{L_1}^2)$

$t_{3/2} = \dfrac{1}{E_2I_2}(\text{Area}_{2-3})\cdot\bar{X}_3$

$t_{3/2} = \dfrac{1}{E_2I_2}\left[ A_2\bar{b}_2 + (\frac{1}{2}M_2L_2)(\frac{2}{3}L_2) + (\frac{1}{2}M_3L_2)(\frac{1}{3}L_2) \right]$

$t_{3/2} = \dfrac{1}{6E_2I_2}(6A_2\bar{b}_2 + 2M_2{L_2}^2 + M_3{L_2}^2)$

Substitute t_1/2 and t_3/2 to equation (1)
$\dfrac{1}{6E_1I_1}\left(\dfrac{6A_1\bar{a}_1}{L_1} + M_1L_1 + 2M_2L_1 \right) + \dfrac{1}{6E_2I_2}\left( \dfrac{6A_2\bar{b}_2}{L_2} + 2M_2L_2 + M_3L_2 \right)$
$= \dfrac{h_1}{L_1} + \dfrac{h_3}{L_2}$

Multiply both sides by 6
$\dfrac{1}{E_1I_1}\left(\dfrac{6A_1\bar{a}_1}{L_1} + M_1L_1 + 2M_2L_1 \right) + \dfrac{1}{E_2I_2}\left( \dfrac{6A_2\bar{b}_2}{L_2} + 2M_2L_2 + M_3L_2 \right)$
$= 6\left( \dfrac{h_1}{L_1} + \dfrac{h_3}{L_2} \right)$

Distribute 1/EI
$\dfrac{6A_1\bar{a}_1}{E_1I_1L_1} + \dfrac{M_1L_1}{E_1I_1} + \dfrac{2M_2L_1}{E_1I_1} + \dfrac{6A_2\bar{b}_2}{E_2I_2L_2} + \dfrac{2M_2L_2}{E_2I_2} + \dfrac{M_3L_2}{E_2I_2} = 6\left( \dfrac{h_1}{L_1} + \dfrac{h_3}{L_2} \right)$

Combine similar terms and rearrange

$\dfrac{M_1L_1}{E_1I_1} + 2M_2\left( \dfrac{L_1}{E_1I_1} + \dfrac{L_2}{E_2I_2} \right) + \dfrac{M_3L_2}{E_2I_2} + \dfrac{6A_1\bar{a}_1}{E_1I_1L_1} + \dfrac{6A_2\bar{b}_2}{E_2I_2L_2} = 6 \left( \dfrac{h_1}{L_1} + \dfrac{h_3}{L_2} \right)$

If E is constant this equation becomes,

$\dfrac{M_1L_1}{I_1} + 2M_2\left( \dfrac{L_1}{I_1} + \dfrac{L_2}{I_2} \right) + \dfrac{M_3L_2}{I_2} + \dfrac{6A_1\bar{a}_1}{I_1L_1} + \dfrac{6A_2\bar{b}_2}{I_2L_2} = 6E \left( \dfrac{h_1}{L_1} + \dfrac{h_3}{L_2} \right)$

If E and I are constant then,

$M_1L_1 + 2M_2(L_1 + L_2) + M_3L_2 + \dfrac{6A_1\bar{a}_1}{L_1} + \dfrac{6A_2\bar{b}_2}{L_2} = 6EI \left( \dfrac{h_1}{L_1} + \dfrac{h_3}{L_2} \right)$

For the application of three-moment equation to continuous beam, points 1, 2, and 3 are usually unsettling supports, thus h₁ and h₃ are zero. With E and I constants, the equation will reduce to

$M_1L_1 + 2M_2(L_1 + L_2) + M_3L_2 + \dfrac{6A_1\bar{a}_1}{L_1} + \dfrac{6A_2\bar{b}_2}{L_2} = 0$

Factors for the three-moment equation
The table below list the value of $6A\bar{a}/L$ and $6A\bar{b}/L$ for different types of loading.

Type of Loading	$\dfrac{6A\bar{a}}{L}$	$\dfrac{6A\bar{b}}{L}$
Concentrated load anywhere on the span.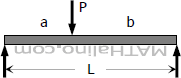	$\dfrac{Pa}{L}(L^2 - a^2)$	$\dfrac{Pb}{L}(L^2 - b^2)$
Concentrated load at the midspan.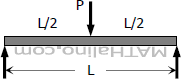	$\dfrac{3PL^2}{8}$	$\dfrac{3PL^2}{8}$
Uniform load over the entire span.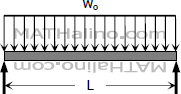	$\dfrac{w_oL^3}{4}$	$\dfrac{w_oL^3}{4}$
Increasing triangular load on the whole span.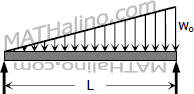	$\dfrac{8w_oL^3}{60}$	$\dfrac{7w_oL^3}{60}$
Decreasing triangular load on the whole span.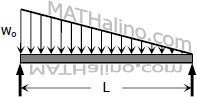	$\dfrac{7w_oL^3}{60}$	$\dfrac{8w_oL^3}{60}$
Isosceles triangular load over the entire span.	$\dfrac{5w_oL^3}{32}$	$\dfrac{5w_oL^3}{32}$
Moment load at any point on the span.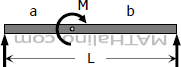	$-\dfrac{M}{L}(3a^2 - L^2)$	$+\dfrac{M}{L}(3b^2 - L^2)$
General uniform loading.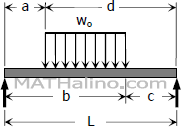	$\dfrac{6A\bar{a}}{L} = \dfrac{w_o}{4L}[ \, b^2(2L^2 - b^2) - a^2(2L^2 - a^2) \, ]$
General uniform loading.	$\dfrac{6A\bar{b}}{L} = \dfrac{w_o}{4L}[ \, d^2(2L^2 - d^2) - c^2(2L^2 - c^2) \, ]$

Navigation

Recent comments