Continuous Beam With Equal Support Reactions

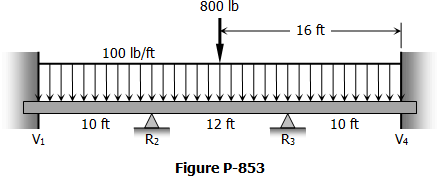
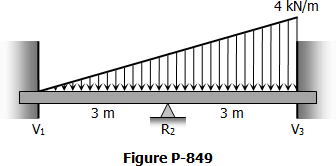
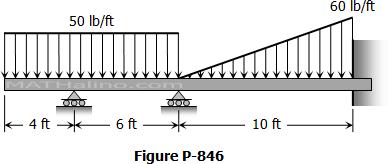
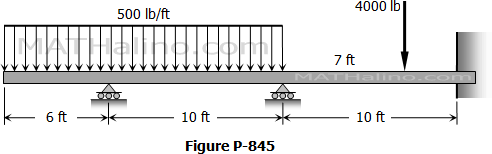
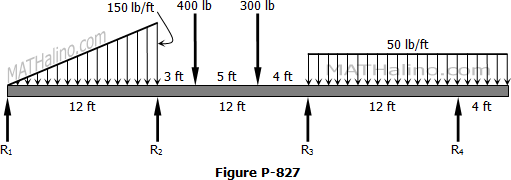
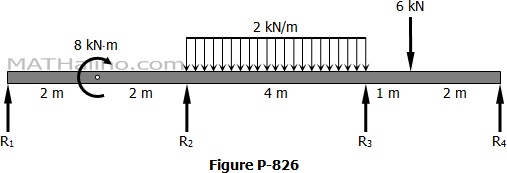
Situation
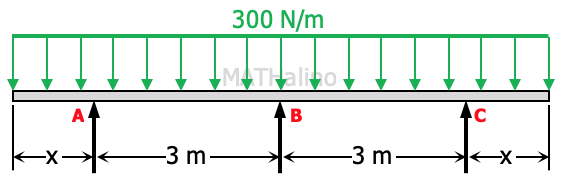
A beam 100 mm × 150 mm carrying a uniformly distributed load of 300 N/m rests on three supports spaced 3 m apart as shown below. The length x is so calculated in order that the reactions at all supports shall be the same.
 

design-practice-2-given.png

 

1.   Find x in meters.

A.   1.319 C.   1.217
B.   1.139 D.   1.127

2.   Find the moment at B in N·m.

A.   -240 C.   -242
B.   -207 D.   -226

3.   Calculate the reactions in Newton.

A.   843.4 C.   863.8
B.   425.4 D.   827.8

 

Continuous Beam With a Gap and a Zero Moment in Interior Support

Situation
A beam of uniform cross section whose flexural rigidity EI = 2.8 × 1011 N·mm2, is placed on three supports as shown. Support B is at small gap Δ so that the moment at B is zero.
 

design-practice-1-given.gif

 

1.   Calculate the reaction at A.

A.   4.375 kN C.   5.437 kN
B.   8.750 kN D.   6.626 kN

2.   What is the reaction at B?

A.   4.375 kN C.   5.437 kN
B.   8.750 kN D.   6.626 kN

3.   Find the value of Δ.

A.   46 mm C.   34 mm
B.   64 mm D.   56 mm