Beam Stiffness (Let I = 60)
Formula: $K = \dfrac{I}{L}$
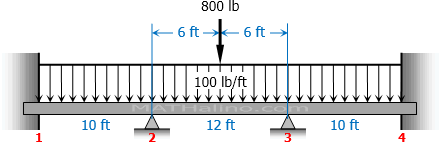
$K_{12} = 60/10 = 6$
$K_{23} = 60/12 = 5$
$K_{34} = 60/10 = 6$
Distribution Factors
Formula: $DF = \dfrac{K}{\Sigma K}$
$DF_{12} = 0$
$DF_{21} = \dfrac{6}{6 + 5} = 6/11$
$DF_{23} = \dfrac{5}{6 + 5} = 5/11$
$DF_{32} = \dfrac{5}{5 + 6} = 5/11$
$DF_{34} = \dfrac{6}{5 + 6} = 6/11$
$DF_{43} = 0$
Fixed End Moments
$\begin{align}
FEM_{12} & = -\dfrac{w_oL^2}{12} \\
& = -\dfrac{100(10^2)}{12} \\
& = -\dfrac{2500}{3} ~ \text{lb}\cdot\text{ft} \\
& = -833.33 ~ \text{lb}\cdot\text{ft}
\end{align}$
$\begin{align}
FEM_{21} & = \dfrac{2500}{3} ~ \text{lb}\cdot\text{ft} \\
& = 833.33 ~ \text{lb}\cdot\text{ft}
\end{align}$
$\begin{align}
FEM_{23} & = -\dfrac{w_oL^2}{12} - \dfrac{PL}{8} \\
& = -\dfrac{100(12^2)}{12} - \dfrac{800(12)}{8} \\
& = -2400 ~ \text{lb}\cdot\text{ft}
\end{align}$
$FEM_{32} = 2400 ~ \text{lb}\cdot\text{ft}$
$\begin{align}
FEM_{34} & = -\dfrac{w_oL^2}{12} \\
& = -\dfrac{100(10^2)}{12} \\
& = -\dfrac{2500}{3} ~ \text{lb}\cdot\text{ft} \\
& = -833.33 ~ \text{lb}\cdot\text{ft}
\end{align}$
$\begin{align}
FEM_{43} & = \dfrac{2500}{3} ~ \text{lb}\cdot\text{ft} \\
& = 833.33 ~ \text{lb}\cdot\text{ft}
\end{align}$
| Joint |
1 |
|
2 |
2 |
|
3 |
3 |
|
4 |
| DF |
0 |
|
6/11 |
5/11 |
|
5/11 |
5/11 |
|
0 |
| FEM |
-833.33 |
|
833.33 |
-2400 |
|
2400 |
-833.33 |
|
833.33 |
| |
427.27 |
← |
854.55 |
712.12 |
→ |
356.06 |
|
|
|
| |
|
|
|
-436.98 |
← |
-873.97 |
-1048.76 |
→ |
-524.38 |
| |
119.18 |
← |
238.35 |
198.63 |
→ |
99.31 |
|
|
|
| |
|
|
|
-22.57 |
← |
-45.14 |
-54.17 |
→ |
-27.09 |
| |
6.16 |
← |
12.31 |
10.26 |
→ |
5.13 |
|
|
|
| |
|
|
|
-1.17 |
← |
-2.33 |
-2.80 |
→ |
-1.40 |
| |
0.32 |
← |
0.64 |
0.53 |
→ |
0.26 |
|
|
|
| |
|
|
|
-0.06 |
← |
-0.12 |
-0.14 |
→ |
-0.07 |
| |
0.02 |
← |
0.03 |
0.03 |
→ |
0.01 |
|
|
|
| |
|
|
|
0.00 |
← |
-0.01 |
-0.01 |
→ |
0.00 |
| |
0.00 |
← |
0.00 |
0.00 |
|
|
|
|
|
| SUM |
-280.39 |
|
1939.22 |
-1939.22 |
|
1939.22 |
-1939.22 |
|
280.39 |
Answer:
M1 = M4 = -280.39 lb·ft
M2 = M3 = -1939.22 lb·ft
Download the Microsoft Excel File
- Download the attached file below.
