fixed-end moment
The Moment Distribution Method
Moment distribution is based on the method of successive approximation developed by Hardy Cross (1885–1959) in his stay at the University of Illinois at Urbana-Champaign (UIUC). This method is applicable to all types of rigid frame analysis.
- Read more about The Moment Distribution Method
- Log in to post comments
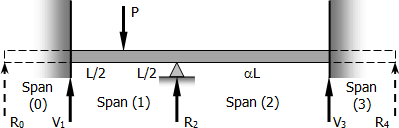
Problem 851 | Continuous Beams with Fixed Ends
Problem 851
Replace the distributed load in Problem 850 by a concentrated load P at the midspan and solve for the moment over the supports.
- Read more about Problem 851 | Continuous Beams with Fixed Ends
- Log in to post comments
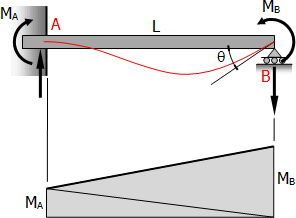
Fixed-end moments of fully restrained beam
Summary for the value of end moments and deflection of perfectly restrained beam carrying various loadings. Note that for values of EIy, y is positive downward.
Case 1: Concentrated load anywhere on the span of fully restrained beam
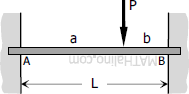 End moments
End moments$M_A = -\dfrac{Pab^2}{L^2}$
$M_B = -\dfrac{Pa^2b}{L^2}$
Value of EIy
$\text{Midspan } EI\,y = \dfrac{Pb^2}{48}(3L - 4b)$
Note: only for b > a
- Read more about Fixed-end moments of fully restrained beam
- Log in to post comments
Problem 738 | Fully restrained beam with moment load
Problem 738
A perfectly restrained beam is loaded by a couple M applied where shown in Fig. P-738. Determine the end moments.
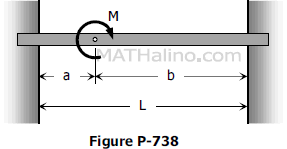
Solution 738
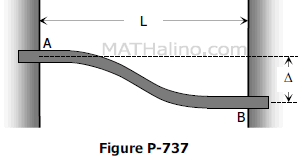
Problem 737 | Fully restrained beam with one support settling
Problem 737
In the perfectly restrained beam shown in Fig. P-737, support B has settled a distance Δ below support A. Show that MB = -MA = 6EIΔ/L2.