Problem 736 | Shear and moment diagrams of fully restrained beam under triangular load
Problem 736
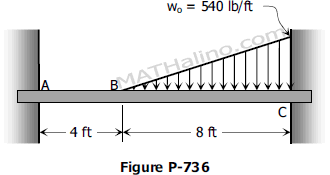
Determine the end shears and end moments for the restrained beam shown in Fig. P-736 and sketch the shear and moment diagrams.
fixed-end moment
Problem 735 | Fixed-ended beam with one end not fully restrained
Problem 735
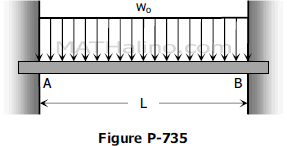
The beam shown in Fig. P-735 is perfectly restrained at A but only partially restrained at B, where the slope is woL3/48EI directed up to the right. Solve for the end moments.
Problem 734 | Restrained beam with uniform load over half the span
Problem 734
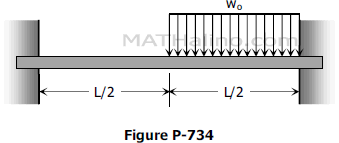
Determine the end moments for the restrained beams shown in Fig. P-734.
Problem 730 | Uniform loads at each end of fully restrained beam
Problem 703
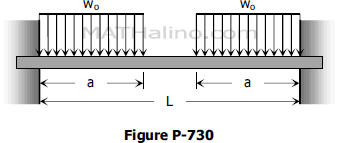
Determine the end moment and maximum deflection for a perfectly restrained beam loaded as shown in Fig. P-730.
Problem 729 | Uniform load over the center part of fixed-ended beam
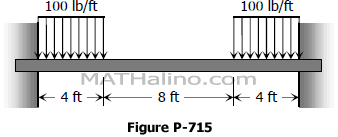
Problem 729
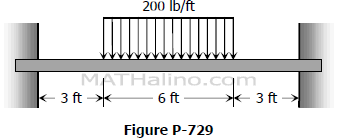
For the restrained beam shown in Fig. P-729, compute the end moment and maximum EIδ.
Problem 728 | Isosceles triangular load over the entire span of fully restrained beam
Problem 728
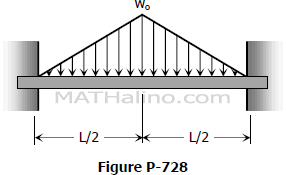
Determine the end moment and maximum deflection of a perfectly restrained beam loaded as shown in Fig. P-728.
Problem 715 | Distributed loads placed symmetrically over fully restrained beam
Problem 12
Determine the moment and maximum EIδ for the restrained beam shown in Fig. RB-012. (Hint: Let the redundants be the shear and moment at the midspan. Also note that the midspan shear is zero.)
