Fixed-end moments of fully restrained beam
Summary for the value of end moments and deflection of perfectly restrained beam carrying various loadings. Note that for values of EIy, y is positive downward.
Case 1: Concentrated load anywhere on the span of fully restrained beam
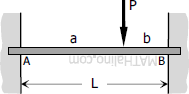End moments$M_A = -\dfrac{Pab^2}{L^2}$
$M_B = -\dfrac{Pa^2b}{L^2}$
$\text{Midspan } EI\,y = \dfrac{Pb^2}{48}(3L - 4b)$
Note: only for b > a
Case 2: Concentrated load on the midspan of fully restrained beam
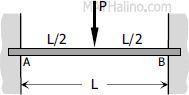End moments$M_A = M_B = -\dfrac{PL}{8}$
Value of EIy
$\text{Maximum } EI\,y = \dfrac{PL^3}{192}$
Case 3: Uniformly distributed load over the entire span of fully restrained beam
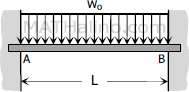End moments$M_A = M_B = -\dfrac{w_oL^2}{12} = -\dfrac{WL}{12}$
Value of EIy
$\text{Maximum } EI\,y = \dfrac{w_oL^4}{384} = \dfrac{WL^3}{384}$
Case 4: Uniformly distributed load over half the span of fully restrained beam
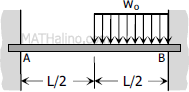End moments$M_A = -\dfrac{5w_oL^2}{192} = -\dfrac{5WL}{96}$
$M_B = -\dfrac{11w_oL^2}{192} = -\dfrac{11WL}{96}$
Value of EIy
$\text{Midspan } EI\,y = \dfrac{w_oL^4}{384} = \dfrac{WL^3}{384}$
Case 5: Triangular load over the entire span of fully restrained beam
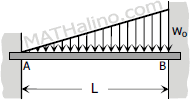End moments$M_A = -\dfrac{w_oL^2}{30} = -\dfrac{WL}{15}$
$M_B = -\dfrac{w_oL^2}{20} = -\dfrac{WL}{10}$
Value of EIy
$\text{Midspan } EI\,y = \dfrac{w_oL^4}{768} = \dfrac{WL^3}{384}$
Case 6: Isosceles triangle loadings over the entire span of fully restrained beam
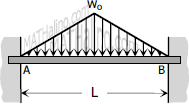End moments$M_A = M_B = -\dfrac{5w_oL^2}{96} = -\dfrac{5WL}{48}$
Value of EIy
$\text{Maximum } EI\,y = \dfrac{7w_oL^4}{3840} = \dfrac{7WL^3}{1920}$
Case 7: Moment load anywhere on the span of fully restrained beam
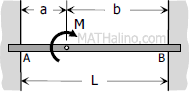End moments$M_A = \dfrac{Mb}{L}\left( \dfrac{3a}{L} - 1 \right)$
$M_B = -\dfrac{Ma}{L}\left( \dfrac{3b}{L} - 1 \right)$
Case 8: Fully restrained beam with one support settling
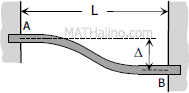End moments$M_A = -\dfrac{6EI \Delta}{L^2}$
$M_B = \dfrac{6EI \Delta}{L^2}$