The overhang is resolved into simple beam with end moments. The magnitude of end moment is,
$M = 2000(2)(1) + 2P$
$M = 4000 + 2P$
Moment of inertia of beam section
$I = \dfrac{bd^3}{12} = \dfrac{4(8^3)}{12}$
$I = \dfrac{512}{3} \, \text{ in}^4$
The midspan deflection is a combination of deflection due to uniform load and two end moments. Use Case No. 8 and Cases No. 8, 11, and 12 to solve for the midspan deflection.
| Type of Loading |
Midspan Deflection |
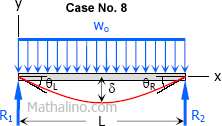 |
$\delta = \dfrac{5w_oL^4}{384EI}$ |
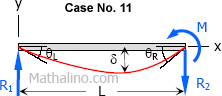 |
$\delta = \dfrac{ML^2}{16EI}$ |
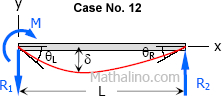 |
$\delta = \dfrac{ML^2}{16EI}$ |
$\delta_{midspan} = \dfrac{5w_oL^4}{384EI} - 2\left[ \dfrac{ML^2}{16EI} \right]$
$0.5 = \dfrac{5(2000)(10^4)(12^3)}{384(1.5 \times 10^6)(\frac{512}{3})} - 2\left[ \dfrac{(4000 + 2P)(10^2)(12^3)}{16(1.5 \times 10^6)(\frac{512}{3})} \right]$
$0.5 = \dfrac{225}{128} - \dfrac{27(4000 + 2P)}{320\,000}$
$160\,000 = 562\,500 - 27(4000 + 2P)$
$27(4000 + 2P) = 402\,500$
$2P = 10\,907.40$
$P = 5453.7 \, \text{ lb}$ answer
