The rotation at the left support is the combination of
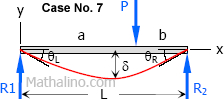
Case No. 7 and
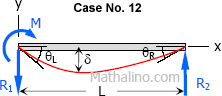
Case No. 12.
| $\theta_L = \dfrac{Pb(L^2 - b^2)}{6EIL}$ |
 |
| $\theta_L = \dfrac{ML}{3EI}$ |
 |
The overhang beam is transformed into a simple beam and the end moment at the free end of the overhang is carried to the left support of the transformed beam.
$\theta = \dfrac{Pb(L^2 - b^2)}{6EIL} - \dfrac{ML}{3EI}$
$\theta = \dfrac{800(1.5)(4.5^2 - 1.5^2)}{6EI(4.5)} - \dfrac{600(4.5)}{3EI}$
$\theta = \dfrac{800}{EI} - \dfrac{900}{EI}$
$\theta = -\dfrac{100}{EI}$
The negative sign indicates that the rotation at the left end contributed by the end moment (taken as negative) is greater than the rotation at the left end contributed by the concentrated load (taken as positive).
From Case No. 5, the end deflection is
$\delta = \dfrac{ML^2}{2EI}$
The deflection at the overhang due to moment load alone is
$\delta_M = \dfrac{600(2^2)}{2EI}$
$\delta_M = \dfrac{1200}{EI}$
Total deflection at the left end of the given beam is
$\delta = 2\theta + \delta_M$
$\delta = 2\left( \dfrac{100}{EI} \right) + \dfrac{1200}{EI}$
$\delta = \dfrac{1400}{EI}$ answer
