end deflection

Solution to Problem 688 | Beam Deflection by Method of Superposition

Problem 688
Determine the midspan value of EIδ at the left end of the beam shown in Fig. P-688.

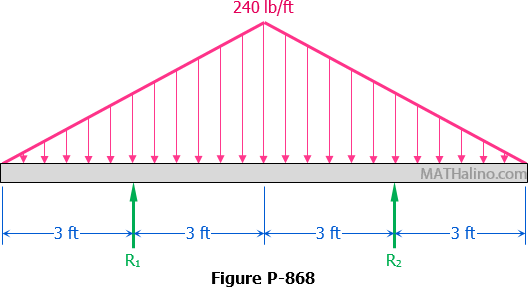
Solution to Problem 666 | Deflections in Simply Supported Beams

Problem 666
Determine the value of EIδ at the right end of the overhanging beam shown in Fig. P-666.

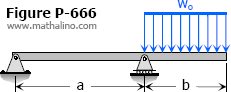
Overhang beam with uniform load at the overhang

Solution to Problem 644 | Deflection of Cantilever Beams

Problem 644
Determine the maximum deflection for the beam loaded as shown in Fig. P-644.

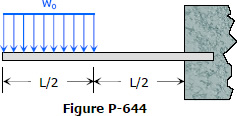
Uniform load over half end of cantilever beam

Solution to Problem 643 | Deflection of Cantilever Beams

Problem 643
Find the maximum value of EIδ for the cantilever beam shown in Fig. P-643.

Solution to Problem 642 | Deflection of Cantilever Beams

Problem 642
Find the maximum deflection for the cantilever beam loaded as shown in Figure P-642 if the cross section is 50 mm wide by 150 mm high. Use E = 69 GPa.

Uniform load over the free end of cantilever beam

Solution to Problem 641 | Deflection of Cantilever Beams

Problem 641
For the cantilever beam shown in Fig. P-641, what will cause zero deflection at A?

Unknown point force P and counterclockwise moment in cantilever beam

Solution to Problem 639 | Deflection of Cantilever Beams

Problem 639
The downward distributed load and an upward concentrated force act on the cantilever beam in Fig. P-639. Find the amount the free end deflects upward or downward if E = 1.5 × 10⁶ psi and I = 60 in⁴.

Cantilever beam with uniform downward load and concentrated upward load

Solution to Problem 638 | Deflection of Cantilever Beams

Problem 638
For the cantilever beam shown in Fig. P-638, determine the value of EIδ at the left end. Is this deflection upward or downward?

Cantilever Beam with Clockwise Moment Load at Midspan

Problem 868 | Deflection by Three-Moment Equation

Solution to Problem 693 | Beam Deflection by Method of Superposition