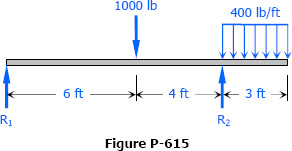
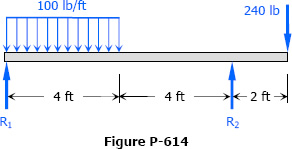
Solution to Problem 636 | Deflection of Cantilever Beams
Problem 636
The cantilever beam shown in Fig. P-636 has a rectangular cross-section 50 mm wide by h mm high. Find the height h if the maximum deflection is not to exceed 10 mm. Use E = 10 GPa.