Solution to Problem 690 | Beam Deflection by Method of Superposition

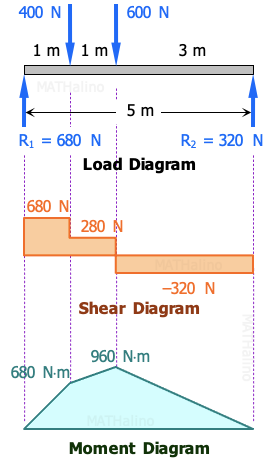
$\Sigma M_{R2} = 0$

$5R_1 = 4(400) + 3(600)$

$R_1 = 680 \, \text{ N}$
 

$\Sigma M_{R1} = 0$

$5R_2 = 1(400) + 2(600)$

$R_2 = 320 \, \text{ N}$
 

Based on allowable flexural stress
$( \, f_b \, )_{max} = \dfrac{6M_{max}}{bd^2}$

$10 = \dfrac{6(960)(1000)}{50d^2}$

$d^2 = 11 \, 520$

$d = 107.33 \, \text{ mm}$
 

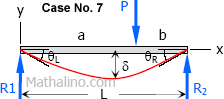Based on allowable midspan deflection. Use Case No. 7, the midspan deflection of simple beam under concentrated load is given by

$\delta = \dfrac{Pb}{48EI}(3L^2 - 4b^2) \text{ when } a \gt b$
 

For the given beam, the midspan deflection is the sum of the midspan deflection of each load acting separately.

$\delta = \sum \dfrac{Pb}{48EI}(3L^2 - 4b^2)$

$20 = \dfrac{400(1)(1000^3)}{48(10\,000I)}[ \, 3(5^2) - 4(1^2) \, ] + \dfrac{600(2)(1000^3)}{48(10\,000I)}[ \, 3(5^2) - 4(2^2) \, ]$

$\dfrac{20(10\,000I)}{1000^3} = \dfrac{400(1)}{48}[ \, 3(5^2) - 4(1^2) \, ] + \dfrac{600(2)}{48}[ \, 3(5^2) - 4(2^2) \, ]$

$\dfrac{I}{5000} = \dfrac{1775}{3} + 1475$

$\dfrac{I}{5000} = \dfrac{6200}{3}$

$I = 10\,333\,333.33$

$\dfrac{bd^3}{12} = 10\,333\,333.33$

$\dfrac{50d^3}{12} = 10\,333\,333.33$

$d^3 = 2\,480\,000$

$d = 135.36 \, \text{ mm}$
 

Use d = 135.36 mm           answer