Simple Beam With Overhang Under Uniform Load

Situation
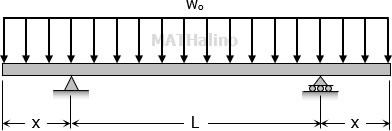
The total length of the beam shown below is 10 m and the uniform load $w_o$ is equal to 15 kN/m.
 

2014-dec-design-simple-beam-with-overhang.jpg

 

1.   What is the moment at midspan if x = 2 m?

A.   37.5 kN·m C.   -187.5 kN·m
B.   -37.5 kN·m D.   187.5 kN·m

2.   Find the length of overhang x, so that the moment at midspan is zero.

A.   2.5 m C.   2.4 m
B.   2.6 m D.   2.7 m

3.   Find the span L so that the maximum moment in the beam is the least possible value.

A.   5.90 m C.   5.92 m
B.   5.88 m D.   5.86 m

 

Simply Supported Beam with Support Added at Midspan to Prevent Excessive Deflection

Situation
A simply supported beam has a span of 12 m. The beam carries a total uniformly distributed load of 21.5 kN/m.
1.   To prevent excessive deflection, a support is added at midspan. Calculate the resulting moment (kN·m) at the added support.

A.   64.5 C.   258.0
B.   96.8 D.   86.0

2.   Calculate the resulting maximum positive moment (kN·m) when a support is added at midspan.

A.   96.75 C.   108.84
B.   54.42 D.   77.40

3.   Calculate the reaction (kN) at the added support.

A.   48.38 C.   161.2
B.   96.75 D.   80.62

 

Support Added at the Midspan of Simple Beam to Prevent Excessive Deflection

Situation
A simply supported steel beam spans 9 m. It carries a uniformly distributed load of 10 kN/m, beam weight already included.

Given Beam Properties:
Area = 8,530 mm2
Depth = 306 mm
Flange Width = 204 mm
Flange Thickness = 14.6 mm
Moment of Inertia, Ix = 145 × 106 mm4
Modulus of Elasticity, E = 200 GPa

1.   What is the maximum flexural stress (MPa) in the beam?

A.   107 C.   142
B.   54 D.   71

2.   To prevent excessive deflection, the beam is propped at midspan using a pipe column. Find the resulting axial stress (MPa) in the column

Given Column Properties:
Outside Diameter = 200 mm
Thickness = 10 mm
Height, H = 4 m
Modulus of Elasticity, E = 200 GPa
A.   4.7 C.   18.8
B.   9.4 D.   2.8

3.   How much is the maximum bending stress (MPa) in the propped beam?

A.   26.7 C.   15.0
B.   17.8 D.   35.6

 

Solution to Problem 581 | Design for Flexure and Shear

Problem 581
A laminated beam is composed of five planks, each 6 in. by 2 in., glued together to form a section 6 in. wide by 10 in. high. The allowable shear stress in the glue is 90 psi, the allowable shear stress in the wood is 120 psi, and the allowable flexural stress in the wood is 1200 psi. Determine the maximum uniformly distributed load that can be carried by the beam on a 6-ft simple span.