Maximum moment for simple beam
$M_{max} = \frac{1}{8} w_o \, L^2$
$M_{max} = \frac{1}{8} w_o \, (6^2)$
$M_{max} = 4.5w_o \, \text{ lb·ft}$
Maximum shear for simple beam
$V_{max} = \frac{1}{2}w_o \, L$
$V_{max} = \frac{1}{2}w_o \, (6)$
$V_{max} = 3w_o \, \text{ lb}$
For bending stress of wood
$f_b = \dfrac{6M}{bd^2}$
$1200 = \dfrac{6(4.5w_o)(12)}{6(10^3)}$
$w_o = 22\,222.22 \, \text{ lb/ft}$
For shear stress of wood
$( \, f_v \, )_{wood} = \dfrac{3V}{2bd}$
$120 = \dfrac{3(3w_o)}{2(6)(10)}$
$w_o = 1600 \, \text{ lb/ft}$
For shear stress in the glued joint
$( \, f_v \, )_{glue} = \dfrac{VQ}{Ib}$
Where:
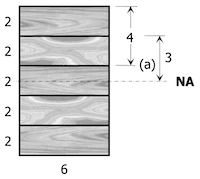
$Q = 6(4)(3.0) = 72 \, \text{ in}^3$
$I = \dfrac{bd^3}{12} = \dfrac{6(10^3)}{12} = 500 \, \text{ in}^4$
$b = 6 \, \text{ in}$
Thus,
$90 = \dfrac{3w_o (72)}{500(6)}$
$w_o = 1250 \, \text{ lb/ft}$
Use wo = 1250 lb/ft for safe value of uniformly distributed load. answer

Q must be 72 if we consider
Q must be 72 if we consider the glued face. y of glued face is 3in from NA.