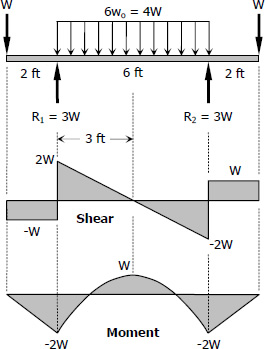
By symmetry
$R_1 = R_2 = \frac{1}{2}(W + 4W +W)$
$R_1 = R_2 = 3W$
$6w_o = 4W$
$w_o = \frac{2}{3}W$
$A = 3(6)(1)$
$A = 18 \, \text{ in}^2$
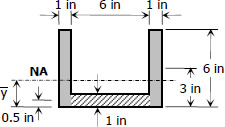
$A\bar{y} = \Sigma ay$
$18\bar{y} = 2 [ \, 6(1)(3) \, ] + 6(1)(0.5)$
$\bar{y} = 2.17 \, \text{ in}$ (okay!)
By transfer formula for moment of inertia
$I_{NA} = 2\left[ \dfrac{1(6^3)}{12} + 6(0.83^2) \right] + \left[ \dfrac{6(1^3)}{12} + 6(1.67^2) \right]$
$I_{NA} = 61.5002 \, \text{ in}^4$ (okay!)
$f_b = \dfrac{Mc}{I}$
For M = -2W lb·ft
Top fiber in tension
$6000 = \dfrac{2W(12)(3.83)}{62}$
$W = 4045 \, \text{ lb}$
Bottom fiber in compression
$10\,000 = \dfrac{2W(12)(2.17)}{62}$
$W = 11\,905 \, \text{ lb}$
For M = W lb·ft
Top fiber in compression
$10\,000 = \dfrac{W(12)(3.83)}{62}$
$W = 13\,490 \, \text{ lb}$
Bottom fiber in tension
$6000 = \dfrac{W(12)(2.17)}{62}$
$W = 14\,286 \, \text{ lb}$
Based on allowable shear stress:
$f_v = \dfrac{VQ}{Ib}$
Where
$V = 2W$
$Q_{NA} = 2 [ \, 3.83(1)(3.83/2) \, ] = 14.6689 \, \text{ in}^3$
$I = 62 \, \text{ in}^4$
$b = 2 \, \text{ in}$
Thus,
$8000 = \dfrac{2W(14.6689)}{62(2)}$
$W = 33\,813 \, \text{ lb}$
For safe value of W, use W = 4045 lb answer
