Solution to Problem 587 | Design for Flexure and Shear

$\Sigma M_{R2} = 0$

$12R_1 + 4P = 16P + 4(3P)$

$R_1 = 2P$
 

$\Sigma M_{R1} = 0$

$12R_2 + 4P = 16P + 8(3P)$

$R_2 = 3P$
 

$W = \frac{1}{2}(12)w_o = 3P$

$w_o = \frac{1}{2}P$
 

To draw the Shear Diagram

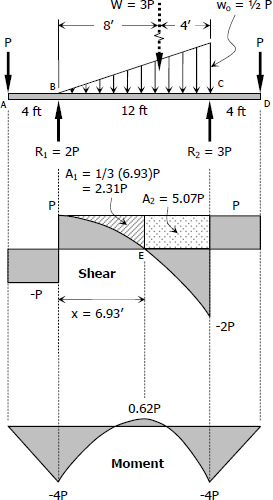
1. V_A = -P lb
2. V_B = V_A + Area in load diagram
   V_B = -P + 0 = -P lb
   V_B2 = V_B + R₁ = -P + 2P = P lb
3. V_C = V_B2 + Area in load diagram
   V_C = P - ½(12)(½P) = -2P lb
   V_C2 = V_C + R₂ = -2P + 3P = P lb
4. V_D = V_C2 + Area in load diagram
   V_D = P + 0 = P
   V_D2 = V_D - P = P - P = 0
5. Shear at AB and CD are rectangular.
6. Shear at BC is parabolic (2nd degree curve).
7. Location of zero shear:
   By squared property of parabola
   x² / P = 122 / 3P
   x = 6.93 ft
   12 - x = 5.07 ft

 

To draw the Moment Diagram

1. M_A = 0
2. M_B = M_A + Area in shear diagram
   M_B = 0 - 4P = -4P lb·ft
3. M_E = M_B + Area in shear diagram
   M_E = -4P + 2/3 (6.93)(P) = 0.62P lb·ft
4. M_C = M_E + Area in shear diagram
   M_C = 0.62P - [ 1/3 (12)3P - 2.31P - 5.07P ]
   M_C = -4P lb·ft
5. M_D = M_C + Area in shear diagram
   M_D = -4P + 4P = 0
6. The moment diagram at AB and CD are straight lines (1st degree curves) while at BC is 3rd degree curve.

 

Based on allowable bending stress
$f_b = \dfrac{Mc}{I}$

Where (From Solution 577)
c = 6 in
I = 350.67 in⁴
 

Thus,
$1200 = \dfrac{4P(12)(6)}{350.67}$

$P = 1461.125 \, \text{ lb}$
 

Based on allowable shear stress
$f_v = \dfrac{VQ}{Ib}$

Where (From Solution 577)
Q = 35.5 in³
I = 350.67 in⁴
b = 0.75 in
 

Thus,
$200 = \dfrac{2P(35.5)}{350.67(0.75)}$

$P = 740.85 \, \text{ lb}$
 

For safe value of P, use P = 740.85 lb.           answer