Solution to Problem 588 | Design for Flexure and Shear

$6R_1 = 4w_o(2)$

$R_1 = \frac{4}{3}w_o \, \text{ N} $
 

$\Sigma M_{R1} = 0$

$6R_2 = 4w_o(4)$

$R_2 = \frac{8}{3}w_o \, \text{ N} $
 

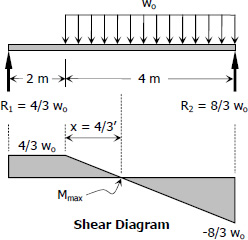
From the shear diagram
$\dfrac{x}{\frac{4}{3}w_o} = \dfrac{4 - x}{\frac{8}{3}w_o}$

$2x = 4 - x$

$x = \frac{4}{3} \, \text{ m}$
 

Maximum moment = sum of area in Shear Diagram at the left of point of zero shear
$M_{max} = 2(\frac{4}{3}w_o) + \frac{1}{2}(\frac{4}{3})(\frac{4}{3}w_o)$

$M_{max} = \frac{32}{9}w_o \, \text{ N}\cdot\text{m}$
 

Based on allowable flexural stress
$f_b = \dfrac{Mc}{I}$

Where
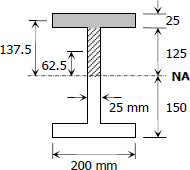
c = 150 mm
I = 200(300³)/12 - 175(250³)/12
I = 222 135 416.67 mm⁴
 

Thus,
$10 = \dfrac{\frac{32}{9}w_o(1000)(150)}{222\,135\,416.67}$

$w_o = 4165.04 \, \text{ N/m}$
 

Based on allowable shear stress
$f_v = \dfrac{VQ}{Ib}$

Where
Q = 200(25)(137.5) + 125(25)(62.5)
Q = 882 812.5 mm³
I = 222 135 416.67 mm⁴
b = 25 mm
 

Thus,
$1.0 = \dfrac{\frac{8}{3}w_o(882 812.5)}{222\,135\,416.67(25)}$

$w_o = 2358.96 \, \text{ N/m}$
 

For safe value of w_o, use w_o = 2358.96 N/m.           answer