Solution to Problem 590 | Design for Flexure and Shear

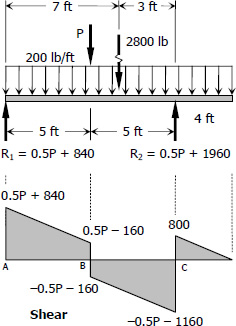
$\Sigma M_{R2} = 0$

$10R_1 = 5P + 3(2800)$

$R_1 = 0.5P + 840$
 

$\Sigma M_{R1} = 0$

$10R_2 = 5P + 7(2800)$

$R_2 = 0.5P + 1960$
 

$M_B = \frac{1}{2} [ \, (0.5P + 840) + (0.5P - 160) \, ](5)$

$M_B = 2.5P + 1700 \, \text{ lb}\cdot\text{ft}$
 

$M_C = M_B - \frac{1}{2} [ \, (0.5P + 160) + (0.5P + 1160) \, ](5)$

$M_C = M_B - (2.5P + 1320)$

$M_C = (2.5P + 1700) - (2.5P + 3300)$

$M_C = -1600 \, \text{ lb}\cdot\text{ft}$
 

Check M_C from the overhang segment
$M_C = -\frac{1}{2}(4)(800)$

$M_C = -1600 \, \text{ lb}\cdot\text{ft}$           (okay!)
 

Based on allowable bending stress
$f_b = \dfrac{Mc}{I}$

Where
M = 2.5P + 1700 lb·ft
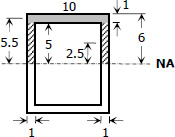
c = 12/2 = 6 in
I = 10(12³)/12 - 8(10³)/12 = 773.33 in⁴
 

Thus,
$1200 = \dfrac{(2.5P + 1700)(12)(6)}{773.33}$

$P = 4475.56 \, \text{ lb}$
 

Based on allowable shear stress
$f_v = \dfrac{VQ}{Ib}$

Where
V = 0.5P + 1160 lb
Q = 10(1)(5.5) + 2 [ 5(1)(2.5) ] = 80 in³
b = 2 in
 

Thus,
$150 = \dfrac{(0.5P + 1160)(80)}{773.33(2)}$

$P = 3480 \, \text{ lb}$
 

For safe value of P, use P = 3480 lb           answer