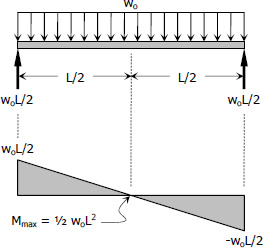
Bending stress:
$f_b = \dfrac{Mc}{I}$
where:
$M = \frac{1}{8}w_o L^2 \, \text{ lb}\cdot\text{ft}$
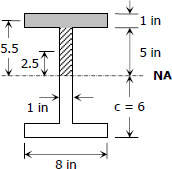
$c = 12/2 = 6 \, \text{ in}$
$I = \dfrac{8(12^3)}{12} - \dfrac{7(10^3)}{12}$
$I = \dfrac{1706}{3} \, \text{ in}^4$
Thus,
$f_b = \dfrac{\frac{1}{8}w_o L^2 (12)(6)}{\frac{1706}{3}}$
$f_b = \frac{27}{1706}w_o L^2$
Shear stress:
$f_v = \dfrac{VQ}{Ib}$
where:
$V = \frac{1}{2}w_o L$
$Q = 8(1)(5.5) + 5(1)(2.5) = 56.5 \, \text{ in}^3$
$I = \frac{1706}{3} \, \text{ in}^4 \,\,$ (see computation above)
$b = 1 \, \text{ in}$
Thus,
$f_v = \dfrac{(\frac{1}{2}w_o L)(56.5)}{\frac{1706}{3}(1)}$
$f_v = \frac{339}{6824}w_o L$
Ratio (flexural stress : shear stress)
$\text{Ratio } = \dfrac{\frac{27}{1706}w_o L^2}{\frac{339}{6824}w_o L}$
$\text{Ratio } = \dfrac{36}{113}L$
$\text{Ratio } = 0.3186L$ answer
