Flexure Formula

Flexure Formula
Stresses caused by the bending moment are known as flexural or bending stresses. Consider a beam to be loaded as shown.

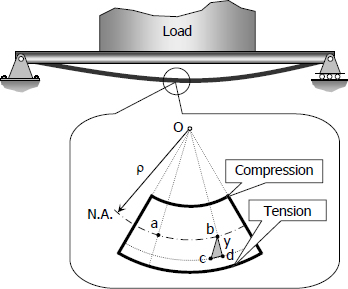
Consider a fiber at a distance $y$ from the neutral axis, because of the beam's curvature, as the effect of bending moment, the fiber is stretched by an amount of $cd$ . Since the curvature of the beam is very small, $bcd$ and $Oba$ are considered as similar triangles. The strain on this fiber is

$\varepsilon = \dfrac{cd}{ab} = \dfrac{y}{\rho}$

By Hooke's law, $\varepsilon = \sigma / E$ , then

$\dfrac{\sigma}{E} = \dfrac{y}{\rho}; \,\, \sigma = \dfrac{y}{\rho}E$

which means that the stress is proportional to the distance $y$ from the neutral axis.

For this section, the notation $f_b$ will be used instead of $\sigma$ .

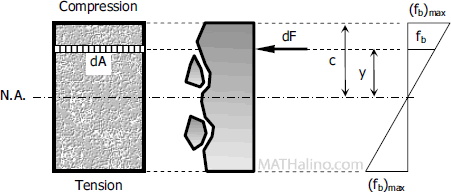
Considering a differential area $dA$ at a distance $y$ from N.A., the force acting over the area is

$dF = f_b \, dA = \dfrac{y}{\rho}E \, dA = \dfrac{E}{\rho}y \, dA$

The resultant of all the elemental moment about N.A. must be equal to the bending moment on the section.

$\displaystyle M = \int dM = \int y\, dF = \int y \, \left( \frac{E}{\rho}y \, dA \right)$

$\displaystyle M = \frac{E}{\rho} \int y^2 \, dA$

but $\int y^2 \, dA = I \,\,$ , then

$M = \dfrac{EI}{\rho} \,\, \text{or} \,\, \rho = \dfrac{EI}{M}$

substituting $\rho = Ey / f_b$

$\dfrac{Ey}{f_b} = \dfrac{EI}{M}$

then

$f_b = \dfrac{My}{I}$

and

$(f_b)_{max} = \dfrac{Mc}{I}$

The bending stress due to beams curvature is

$f_b = \dfrac{Mc}{I} = \dfrac{\dfrac{EI}{\rho}c}{I}$

$f_b = \dfrac{Ec}{\rho}$

The beam curvature is:

$k = \dfrac{1}{\rho}$

where $\rho$ is the radius of curvature of the beam in mm (in), $M$ is the bending moment in N·mm (lb·in), $f_b$ is the flexural stress in MPa (psi), $I$ is the centroidal moment of inertia in mm⁴ (in⁴), and $c$ is the distance from the neutral axis to the outermost fiber in mm (in).

Navigation

Recent comments