Solution to Problem 508 | Flexure Formula

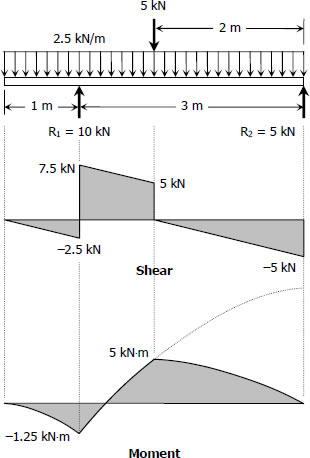
$\Sigma M_{R2} = 0$

$3R_1 = 2(5) + 2(2.5)(4)$

$R_1 = 10 \, \text{kN}$
 

$\Sigma M_{R1} = 0$

$3R_2 = 1(5) + 1(2.5)(4)$

$R_2 = 5 \, \text{kN}$
 

$f_b = \dfrac{Mc}{I}$
 

Where:
$f_b = 20 \, \text{MPa}$

$M = 5 \, \text{kN}\cdot\text{m} = 5(1000)^2 \, \text{N}\cdot\text{mm}$

$c = \frac{1}{2}h$

$I = \dfrac{bh^3}{12} = \dfrac{80h^3}{12} = \frac{20}{3}h^3$
 

Thus,
$20 = \dfrac{5(1000)^2(\frac{1}{2}h)}{\frac{20}{3}h^3}$

$h^2 = 18\,750$

$h = 137 \, \text{mm}$           answer